Chaînes aimantées
CHAPITRE UN
PÔLES ET CHARGES
1.1 Les connaissances électriques et magnétiques avant Gilbert
Les Grecs de l'Antiquité connaissaient l'effet de la magnétite, un minerai de fer trouvé à l'état naturel: celle-ci attire à distance un autre bloc de magnétite ou un objet en fer. Ils connaissaient également la propriété de l'ambre, une résine très dure et de couleur jaune-brun: celle-ci, une fois frottée, attire à distance des petits fétus de paille. Ces deux objets sont les seuls qu'ils connaissaient qui agissent à distance sur d'autres corps; en effet, les autres forces connues sont toutes des forces de contact, forces appliquées directement sur l'objet en question, comme pour pousser une charrette ou la tirer.
Une autre propriété de la magnétite est de toujours pointer dans la même direction lorsque laissée libre de s'orienter à sa guise. Celle-ci est exploitée vers l'an mil après Jésus-Christ: un petit bloc de magnétite est placé dans une petite barque qui flotte dans un bol d'eau; le bloc est ainsi libre de s'orienter à sa guise et cela, toujours dans la même direction, vers l'est par exemple. Nous voici avec le premier modèle de boussole, utilisé par les Chinois pour s'orienter dans les vastes steppes de l'Asie.
Une troisième propriété de la magnétite est de pouvoir fournir cette vertu d'orientation à une aiguille de fer. La magnétite est glissée sur l'aiguille de fer, d'une extrémité à l'autre, dans un mouvement continu: l'aiguille devient alors un aimant. Elle s'oriente, si laissée libre, selon la longitude. Ces aiguilles, placées dans des petits vaisseaux flottants à la surface de l'eau d'un bocal, sont utilisées vers 1200 en France. En 1269, Petrus Peregrinus de Maricourt décrit ce compas flottant et en mentionne un tout nouveau, placé sur un pivot.
Peregrinus façonne un bloc de magnétite en forme de boule. Il l'examine à l'aide d'un petit compas fait d'une aiguille aimantée placée sur un pivot. Il trace, en tout point sur la surface de la boule de magnétite, des lignes correspondant à l'orientation de son compas. Il trouve que les lignes qu'il a tracées sont analogues aux longitudes tracées sur un globe terrestre; celles-ci ont deux points de rencontre, en opposition, comme dans le cas du globe terrestre. Il les nomme pôles par analogie avec les deux pôles de la Terre.
Il trouve que tout aimant, artificiel comme dans le cas de l'aiguille aimantée ou naturel comme dans le cas de la magnétite, a toujours deux pôles. Il remarque de plus que le mouvement des aimants ne dépend que de la position de leurs pôles: c'est donc là que se trouvent les centres de leur puissance magnétique.
1.2 La contribution de Gilbert au magnétisme
William Gilbert (1540-1603) entreprend de passer en revue toutes les connaissances des Anciens sur l'électricité et le magnétisme, de les vérifier et de les compléter. Il publie en 1600 De Magnete, le fruit de ses recherches. Il y reprend les expériences de Peregrinus sur le globe de magnétite. Il appelle pôle nord le pôle du globe aimanté qui pointe librement vers le nord de la Terre, et pôle sud celui du globe aimanté qui pointe vers le pôle sud de la Terre. Il fait de même avec les pôles de l'aiguille de fer aimantée. Il remarque que les pôles des aimants ne sont pas des points mais des régions plus ou moins étendues.
Gilbert remarque de plus que les pôles nord de deux aimants se repoussent, comme d'ailleurs leurs pôles sud, alors que le pôle nord de l'un attire le pôle sud de l'autre, expliquant ainsi leur mouvement l'un vers l'autre. Il remarque de plus que l'attraction entre des pôles opposés augmente avec leur proximité.
Gilbert argumente que si le pôle nord d'un aimant pointe vers le nord géographique de la Terre, c'est que ce point de la Terre l'attire. Or le pôle nord d'un aimant n'est attiré que par le pôle sud d'un autre aimant. Il s'ensuit que la Terre doit agir comme un énorme aimant, avec son pôle sud magnétique à la position de son pôle nord géographique. Tout comme son globe de magnétite agit sur le compas qu'il place à sa surface, la Terre agit sur un compas et en fait pointer le pôle nord vers son nord géographique.
Gilbert remarque de plus qu'une aiguille aimantée, originellement avec un pôle nord à une extrémité et un pôle sud à l'autre, forme deux aimants complets une fois brisée: les deux pôles manquants apparaissent alors. Tout comme deux aiguilles aimantées semblent ne former qu'un seul aimant lorsque placées bout à bout, avec un pôle nord en contact avec un pôle sud.
Il remarque que tous les corps attirés par les aimants possèdent du fer, comme d'ailleurs la magnétite, qui est un minerai de fer déjà aimanté. Il remarque que certains fers font de bons aimants permanents: les aciers, par exemple. Ces fers sont dits aigres. Les autres fers, qui ne font pas de bons aimants permanents, sont dits doux. Les fers, doux et aigres, sont attirés par les aimants, naturels et artificiels.
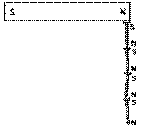
Chaînes aimantéesIl remarque que tout aimant a, en quelque sorte, une zone d'influence qui s'étend à quelque distance de lui. Si un fer se trouve dans cette zone, il va être attiré vers l'aimant. Il remarque que le fer originellement non aimanté est toujours attiré, contrairement au cas d'un aimant placé dans cette même zone qui pourrait être repoussé si ce sont des pôles semblables qui sont les plus proches. Puisque ce sont des pôles magnétiques qui s'attirent ou se repoussent, il s'ensuit que le fer, maintenant dans la zone d'influence de l'aimant, a été aimanté par lui, de telle sorte qu'il lui présente un pôle non semblable. Il explique ainsi les chaînes de clous de fer doux qui traînent à la suite d'un aimant: chacun est aimanté par le précédent, mais un peu plus faiblement. Il remarque que la zone d'influence de l'ensemble est bien plus grande que la zone d'influence de l'aimant original. Cet effet est mentionné, sans essai d'explication, par Platon (428-348), dans son Ion, où il note qu'Euripide (480-406) nomme la pierre aimantée originale magnétique.
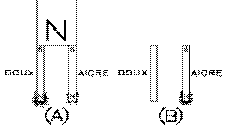
Si le fer, aimanté une fois placé dans la zone d'influence d'un autre aimant, est doux, il va perdre son aimantation une fois l'aimant enlevé. Mais s'il est aigre, il va conserver une partie de son aimantation. Les deux fers, doux et aigres, attirent donc de la limaille de fer quand ils sont dans la zone d'influence d'un aimant (cas A). Mais, une fois celui-ci enlevé (cas B), le fer doux n'attire plus la limaille, alors que le fer aigre continue de l'attirer, démontrant qu'il agit encore comme un aimant. Ce qui démontre que le fer aigre peut faire un aimant permanent, contrairement au fer doux.
Il remarque de plus que placer des capuchons de fer doux contre la magnétite en augmente la capacité de soulever des masses de fer, ce qu'il appelle armer la magnétite.
1.3 La contribution de Gilbert à l'électricité
Les Grecs, avons-nous vu, avaient remarqué que l'ambre frotté attire des fétus de paille. Gilbert remarque que le jais, les pierres précieuses, le verre, le soufre, la cire et la résine, une fois frottés, attirent également les fétus de paille. Le terme grec pour ambre est èlectron: il appelle donc électriques ces corps qui, comme l'ambre, attirent les fétus de paille. Nous appellerons plutôt électrique le phénomène en question, et non le type de corps qui le cause.
Gilbert décide d'examiner en quoi le phénomène magnétique diffère du phénomène électrique: le magnétisme n'a pas besoin de frottement pour exister, contrairement au phénomène électrique. Il remarque de plus qu'une feuille de papier placée entre le corps électrisé par frottement et le fétus de paille réduit son effet sur ce dernier. Il remarque surtout que le corps électrisé attire tous les corps (légers), quelle que soit leur composition, contrairement aux corps magnétiques qui n'attirent que les corps à teneur de fer. Il invente le compas électrique, une aiguille de métal très fine placée sur un pivot. Il remarque que celle-ci pointe toujours dans la direction du corps électrisé s'il est suffisamment proche de cette dernière. C'est donc que l'aiguille métallique est attirée par le corps électrisé.
Il remarque qu'il existe, autour du corps électrisé, une zone d'influence, dans laquelle sa boussole électrique est affectée, tout comme il existe une zone d'influence dans laquelle une boussole normale est affectée par un aimant.
Gilbert remarque de plus que l'électrisation d'un corps est perdue avec le temps, contrairement à la magnétisation d'un aimant fait de fer aigre. Et que cette électrisation disparaît si le corps est humide. Ses expériences électriques ne fonctionnent que par des jours de temps sec, remarque-t-il. Et s'il ne souffle pas avec son haleine (humide) sur le corps électrisé.
1.4 Conducteurs et isolants
En 1660, Otto von Guericke (1602-1686) met au point la première machine électrostatique. Il produit, par moulage, une sphère de soufre traversée par un axe. Il la fait tourner de telle sorte qu'elle frotte contre sa main. Il remarque que le globe produit des petites étincelles en plus d'attirer les fétus de paille. Une plume d'oiseau, remarque-t-il, est d'abord attirée par sa boule électrisée, tout comme les fétus de paille. Mais après avoir touché la boule, elle s'en éloigne, comme si elle était maintenant repoussée: elle peut, dans certains cas, flotter au-dessus du globe de soufre.
En 1729, Stephen Gray (1670-1736) informe Jean Théophile Desaguliers (1683-1744) que l'électrisation de son bâton de verre, due au frottement, peut être transportée à distance à l'aide d'un fil de chanvre qui lui est attaché, mais qu'elle est perdue si le fil de chanvre touche le sol. Par contre, si celui-ci est suspendu par des fils de soie, l'électrification peut être transportée sur une distance d'au moins 100 m. Son problème est que son fil de chanvre n'est pas assez solide. Aussi tente-t-il la même expérience avec des fils métalliques: il remarque que l'électrification se transporte beaucoup mieux à travers le fil en question. Desaguliers nomme en 1736 conducteurs les corps qui transportent ainsi l'électrification; les corps qui ne transportent pas l'électrification, comme le fil de soie, sont des isolants. En fait, les corps comme l'ambre, le soufre, le jais, les pierres précieuses, sont tous des isolants: ils gardent en place l'électrification qui y a été produite par frottement. L'électrification doit donc être un fluide qui coule dans (ou sur) les conducteurs et qui est emprisonné dans (ou sur) les isolants.
En 1729, Gray fabrique deux cubes en chêne, l'un plein, l'autre creux. Il les frotte de la même façon pour les électriser. Il remarque ensuite que les deux cubes attirent des petits objets métalliques exactement de la même façon; ce qui n'est le cas que si le fluide électrique est emprisonné sur (ou très proche) de la surface du cube. La répartition du fluide électrique est donc essentiellement superficielle dans le cas des isolants frottés en surface.
Charles François de Cisternay Du Fay (1698-1739) reprend les expériences de Gray en 1733. Il remarque qu'une mince feuille d'or, suspendue par un isolant, est attirée par un bâton de verre électrifié par frottement (comme l'aurait d'ailleurs remarqué Gilbert en 1600). Mais si son bâton touche la feuille d'or, celle-ci, au lieu d'être attirée, est maintenant repoussée (comme la plume dans l'expérience de Guericke). L'électrification cause ici une force de répulsion, comme dans le cas des pôles semblables de deux aimants. C'est évidemment le fluide électrique qui provient du bâton de verre que reçoit la feuille d'or, comme dans l'expérience des conducteurs de Gray. Il s'ensuit que l'électrification produite par frottement sur le verre repousse l'électrification produite également par frottement sur le verre.
Il remarque maintenant qu'un bâton de résine dont l'électrification est produite par frottement attire la feuille d'or dont l'électrification provient du frottement sur le verre. Et, finalement, que l'électrication produit par frottement sur la résine, une fois transférée sur la feuille d'or, en cause la répulsion. Du Fay conclut donc qu'il y a deux types d'électrifications: l'électricité vitreuse (due au frottement contre le verre et le cristal) et l'électricité résineuse (due au frottement contre la résine, ainsi que la soie, l'ambre, le papier); que l'électricité résineuse attire l'électricité vitreuse comme les pôles sud attirent les pôles nord, et que les électricités vitreuses se repoussent, comme les pôles nord se repoussent, et que les électricités résineuses se repoussent, comme les pôles sud se repoussent.
On produit des machines électrostatiques, supérieures à celle de Guericke, où l'électrification est produite par frottement de la boule de soufre contre un linge caoutchouté et lui est soutirée par une languette de métal flexible en contact avec une sphère métallique isolée du sol. Lorsque la boule de soufre est mise en rotation, le fluide électrique est accumulé sur la sphère métallique qui, alors, peut attirer très facilement les fétus de paille. Au fur et à mesure que davantage de fluide électrique est accumulé, des crépitements se font entendre. Toucher à la sphère cause des chocs électriques.
Si une autre sphère métallique, reliée au sol, est placée proche de la première, des étincelles se produisent à intervalles à peu près réguliers alors que la boule de soufre est tournée à vitesse régulière. Ces étincelles sont accompagnées d'un bruit sec. On remarque que la largeur de l'étincelle produite, sa luminosité et la force du bruit dépendent de la grosseur des sphères utilisées: elles augmentent avec la grosseur des sphères. On remarque de plus qu'éloigner les sphères a pour effet d'augmenter le temps entre les étincelles, et que celles-ci sont alors plus longues. Ce que remarque Du Fay en 1737. Il remarque de plus qu'une mince feuille d'or, flexible, en contact avec une feuille de métal fixe verticale, reliée à la sphère, s'écarte de plus en plus de la verticale au fur et à mesure que la sphère est chargée de fluide électrique par la machine électrostatique. Mais qu'elle retombe à la verticale après l'étincelle, pour reprendre le même cycle. Plus la sphère est chargée de fluide électrique, plus il y en a sur les deux feuilles métalliques, et plus la feuille mobile s'éloigne par répulsion. Celle-ci retombe après l'étincelle; la sphère a alors perdu son fluide électrique: l'étincelle est donc la manifestation dans l'air de l'écoulement du fluide électrique.
Il remarque également que le fluide électrique accumulé sur la sphère se perd avec le temps après l'arrêt de la machine (avant la production de l'étincelle). Évidemment, une façon pour la sphère de perdre son fluide électrique est qu'un individu la touche: ce qu'il ressent alors comme un choc électrique.
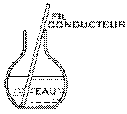Bouteille de Leyde originale
En 1745, Pieter van Musschenbroek (1692-1761), habitant de la ville de Leyde, cherche à contrer ce problème de la perte d'électrisation des corps placés à l'air libre (aussi dit déperdition de l'électricité). Il décide d'emprisonner le fluide électrique à l'intérieur d'une bouteille de verre remplie d'eau et placée sur le plancher en reliant la sphère à l'eau de sa bouteille par un fil conducteur. Il arrête la machine électrostatique juste avant que l'étincelle ait lieu dans cette nouvelle situation. Il touche la sphère reliée à sa bouteille après quelque temps pour voir si la perte de fluide électrique a été réduite: il prend un choc violent, beaucoup plus fort que les autres! C'est donc que celle-ci possédait encore une quantité énorme de fluide électrique.
Cette bouteille est nommée bouteille de Leyde par Jean-Antoine Nollet (1700-1770). Les étincelles produites par une sphère sont beaucoup plus larges, brillantes et le bruit qui les accompagne est beaucoup plus fort lorsque cette bouteille est reliée à la sphère que lorsqu'elle ne l'est pas. C'est donc que la quantité de fluide électrique, qui cause la brillance de l'étincelle et son bruit lorsqu'elle s'écoule dans l'air, est beaucoup plus grande dans le cas où la bouteille de Leyde est reliée à la sphère que dans le cas où elle ne l'est pas. La bouteille de Leyde doit donc accumuler facilement une grande quantité de fluide électrique.
1.5 Le modèle électrique de Franklin
Benjamin Franklin (1706-1790) examine les expériences faites jusqu'ici et en ajoute de nouvelles. En 1747, dans une première expérience, un premier individu, A , isolé du sol par une couche de cire, frotte un tube de verre avec une feuille de caoutchouc et l'électrifie. Un second individu, B , isolé lui-aussi du sol par la couche de cire, touche le tube de verre pour en recueillir la charge. Franklin remarque alors que A donne un choc à un troisième C en contact avec le sol juste avant de le toucher; et que B donne un choc à C dans la même condition.
Dans une seconde expérience, toujours sur la couche de cire afin de rester isolés du sol, A et B se touchent. A frotte alors avec le caoutchouc le tube de verre que tient B . Franklin note que, ni l'un, ni l'autre ne donnent de choc à C en contact avec le sol juste avant de le toucher.
Franklin explique ces résultats ainsi: l'électricité est normalement présente dans une même proportion dans la matière. Dans la première expérience, le frottement du verre par le caoutchouc transfère du fluide électrique de A au verre, puis par attouchement, du verre à B. Il s'ensuit que A manque maintenant de fluide électrique, et que B en a de trop. C en a juste la bonne proportion. L'étincelle subie a comme rôle d'égaliser la distribution d'électricité entre les deux corps qui vont se toucher puisqu'elle est due à un mouvement de fluide électrique. Dans la seconde expérience, le frottement du verre par le caoutchouc transfère du fluide électrique de A au verre, puis du verre à B par attouchement, mais de B à A à nouveau comme ceux-ci se touchent durant l'opération. C'est pourquoi les trois individus, ayant même proportion d'électricité, ne se donnent pas de choc.
Dans chaque cas, le fluide électrique gagné par le verre est perdu par le caoutchouc. Il y a donc conservation du fluide électrique. Remarquons que pour Franklin le fluide électrique n'est que d'un type. Puisque B dans sa première expérience en a de trop, Franklin dit que sa quantité d'électricité est positive. (Il est chargé positivement.) Et puisque A, dans sa première expérience, a perdu du fluide électrique, Franklin dit que sa quantité d'électricité est négative. (Il est chargé négativement.)
Du Fay aurait dit, lui, que l'électricité que porte B est vitreuse (comme elle provient de l'électrification du verre) et que celle portée par A est résineuse (comme elle provient de l'électrification du caoutchouc). Il nous est donc possible d'identifier l'électrification vitreuse de Du Fay avec l'électricité positive de Franklin, et l'électrification résineuse de Du Fay avec l'électricité négative de Franklin. Mais il reste une différence conceptuelle: pour Franklin il n'y a qu'un seul fluide électrique; pour Du Fay, il y en a deux.
Pour Franklin donc, ce qui se déplace dans un conducteur est un fluide électrique qui, lorsqu'accumulé, est une charge positive. Ce qui revient à dire que ce sont les charges positives (associées à l'électricité vitreuse) qui se déplacent. Pourquoi avoir fait ce choix? Pourquoi ne pas avoir associé la charge positive à l'électricité résineuse et avoir ainsi postulé que ce sont les charges associées à l'électricité résineuse qui se déplacent dans les conducteurs?
Si sa sphère est chargée par sa machine électrostatique avec de l'électrification vitreuse, il remarque qu'elle produit des aigrettes après un certain temps de charge, s'il n'y a pas de seconde sphère qui peut lui faire faire une étincelle. Ces aigrettes sont de petites étincelles qui se perdent dans l'air. Si sa sphère est chargée avec de l'électrification résineuse, il observe une étoile à la surface de la sphère, au lieu d'une aigrette. Il interprète ses résultats ainsi: l'aigrette, comme l'étoile, est due au passage du fluide électrique dans l’air. Dans le premier cas, celui de l'aigrette, le fluide électrique va de la sphère chargée vers l'air comme l'étincelle, partie de la sphère, se perd dans l'air; dans le second cas, celui de l'étoile, le fluide électrique va de l'air vers la sphère comme s'il y faisait une éclaboussure, d'où la forme d'une étoile. Le fluide électrique a quitté la sphère chargée par frottement contre le verre parce que sa proportion y était trop forte; et est venu frapper la sphère chargée par frottement avec le caoutchouc parce que sa proportion y était trop faible. Il s'ensuit que le cas d'un surplus de fluide électrique est associé à l'électrification par le verre et le manque, à l'électrification résineuse.
Dans la nomenclature de Franklin, des charges de même type sont de même signe et se repoussent; et des charges de types différents sont de signes opposés et s'attirent. Nous allons essentiellement utiliser cette nomenclature à partir de maintenant.
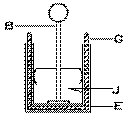Bouteille de Leydemodifiée
Sir William Watson (1715-1787) modifie la bouteille de Leyde: elle est maintenant formée par trois gobelets, placés l'un dans l'autre et en contact: un gobelet métallique interne J (relié à un conducteur B ) en contact avec la surface interne d'un gobelet de verre G , lui-même en contact avec la surface interne d'un gobelet métallique externe E .
Franklin comprend que l'un des deux gobelets métalliques a un excédent du fluide électrique et l'autre, le manque correspondant (de telle sorte que la charge de l'un égale, au signe près, la charge de l'autre). Mais cela n'est pas suffisant pour expliquer la quantité de fluide électrique accumulé: il faut, montre-t-il, qu'une grande partie de celui-ci se trouve dans le verre placé entre les deux gobelets métalliques. Mais, sait-il, le verre est un isolant, et donc est imperméable au fluide électrique. Il faut donc que le fluide électrique associé au verre soit placé sur ses surfaces en contact avec une surface métallique, et que ce soit par cette surface métallique que le fluide puisse se déplacer. Encore une fois, la charge est superficielle pour un isolant.
1.6 Le pouvoir des pointes
Franklin examine en 1747 les étincelles produites entre deux sphères métalliques de grand rayon de courbure comparées à la distance entre elles, une reliée à la terre, l'autre à sa machine électrostatique. Il remarque que les étincelles ne vont pas des mêmes points sur chacune des sphères, mais de points différents, à chaque fois. Mais s'il monte sur l'une d'elles une courte pointe métallique, il remarque qu'il ne lui est plus possible de produire des étincelles entre ces deux sphères toujours à même distance, mais que des aigrettes ou étoiles sont produites à la pointe: le fluide électrique n'a pas la chance de s'accumuler suffisamment sur les sphères pour causer des étincelles, puisqu'il s'écoule à la pointe.
Franklin remarque les similarités entre les étincelles et la foudre: dans chaque cas, un canal très brillant apparaît. Le son qui accompagne l'étincelle est fort semblable à celui qui accompagne la foudre qui tombe très proche. Il considère donc que la foudre est une gigantesque étincelle.
En 1752, durant un orage, il collecte du fluide électrique d'un nuage, à l'aide d'un conducteur qu'il a fait monter vers lui à l'aide d'un cerf-volant, et le recueille dans une bouteille de Leyde; il montre que la charge due à celle-ci a les mêmes effets que celle produite par une machine électrostatique.
Franklin imagine alors le paratonnerre: un fil conducteur relié à la terre dont l'autre extrémité, pointue, surplombe le bâtiment qu'il protège. Il suppose que la charge dans le nuage va attirer, de la terre dans le paratonnerre, des charges opposées qui vont donc se concentrer dans la pointe du paratonnerre; là, elles vont causer des aigrettes (ou des étoiles) et ainsi le fluide électrique va couler entre le nuage et le sol avant que l'accumulation de charges devienne telle que la foudre ne frappe. Il met donc à profit l'effet de pointe d'un conducteur: le fluide électrique en coule très facilement.
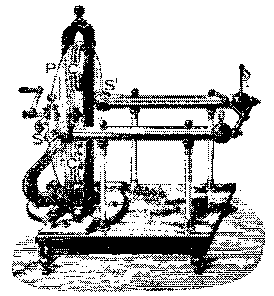Machine de RamsdenJesse Ramsden (1735-1800) invente en 1766 une machine électrostatique supérieure qui porte son nom. Déjà sir Isaac Newton (1642-1727) avait fabriqué une machine électrostatique qui utilisait un disque isolant en rotation au lieu d'une sphère, et le verre comme isolant frotté, au lieu du soufre. Un disque de verre P est frotté, lors de sa rotation, contre deux coussinets C et C' , revêtus d'or massif, placés le long de son diamètre (la verticale ici), de part et d'autre de son axe. Le verre s'électrise alors positivement par frottement contre les coussinets d'or. La partie chargée du verre continue sa rotation et rencontre deux peignes de métal S et S' très proches du disque, placés de part et d'autre de l'axe de rotation selon un diamètre perpendiculaire à celui des coussinets (l'horizontale ici). Les peignes métalliques sont formés d'une série de pointes. Des charges négatives sont alors attirées aux extrémités des pointes par les charges positives sur le verre, comme dans le cas de la pointe du paratonnerre. Il y a donc formation d'aigrettes entre le disque chargé et les pointes du peigne: la charge du verre est alors comme transférée au peigne métallique relié à l'objet conducteur à charger. Ce processus fonctionne aussi longtemps que le disque est en rotation.
1.7 La charge par influence
a) induction
En 1753, John Canton (1718-1772) colle, aux points D et C d'un conducteur allongé B isolé du sol, deux petites feuilles d'or de telle sorte que celles-ci puissent s'éloigner de la surface qui leur est voisine si celle-ci est chargée, puisque le signe de leur charge sera alors le même que celui de la surface avoisinante. Il s'assure que le corps B est bien initialement déchargé en plaçant son doigt dessus. (Rappelons-nous que le corps humain est un conducteur.) Les deux feuilles d’or sont alors verticales.
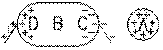Induction du conducteur BIl approche, mais sans y toucher, un corps chargé A (disons positivement). Il remarque que la partie C du conducteur allongé isolé B , celle la plus proche du corps chargé A , possède une charge; sa partie la plus éloignée D , également: ceci puisque les feuilles d'or placées en ces régions sont repoussées. Il touche le corps en C avec une autre feuille d'or, placée sur un manche isolant, et l'approche toute seule de A ; il remarque qu'elle est attirée, ce qui nécessite que sa charge soit de signe opposé à celle de A (soit négative, dans notre cas). Il trouve que le signe de la charge en D de la même façon en remarquant que la feuille d'or, placée sur un manche isolant, approchée de A après avoir été mise en contact avec D , est repoussée par A et donc est de même signe (soit dans notre cas, positive).
Il comprend que le fluide électrique du corps allongé B s'est déplacé sous l'action de la charge du corps extérieur A , de telle sorte que la charge nette du corps B demeure la même: le gain de fluide électrique d'une partie est dû à la perte de fluide électrique de l'autre. Ces charges ne sont pas apparues par frottement mais bien par l'action à distance des charges du corps extérieur A . Les charges du corps A causent une force électrique qui est ressentie à distance par d'autres charges, comme les corps matériels causent une force gravitationnelle qui est ressentie à distance par d'autres corps matériels. (La loi de la gravitation de sir Isaac Newton, qui montre que la force gravitationnelle va comme l'inverse du carré de la distance entre deux corps, publiée en 1687 dans son Principia, est la seule autre sorte de force alors connue avec la force magnétique qui agit également à distance.)
Le corps chargé extérieur A , peut-il remarquer, a une zone d'influence, zone dans laquelle il peut agir sur le conducteur B et y induire des charges en déplaçant assez de fluide électrique pour que cet effet soit mesurable. Cette zone d'influence mesurable porte le nom de champ électrique. (Ce terme n'apparaît en fait que beaucoup plus tard.)
Un conducteur, placé dans le champ électrique d'une charge externe, voit donc son fluide électrique mis en mouvement de telle sorte que les charges induites proches de la charge externe soient de signes opposés à celle-ci; dans notre cas où la charge externe est positive, le fluide électrique est repoussé par celle-ci. Nous pouvons définir le sens de l'action de la charge externe sur le fluide électrique du conducteur: il s'éloigne de la charge qui la cause si celle-ci est positive et s'en approche si celle-ci est négative. Nous savons déjà que l'action d'une charge sur le fluide électrique d'un conducteur diminue en fonction de sa distance. La zone d'une certaine influence électrique va donc être limitée pour une charge. Mais celle-ci est plus grande si la charge est plus grande.
Plus l'influence électrique d'une charge est grande donc, plus il y a de mouvement du fluide électrique dans un conducteur. Mais voilà que le mouvement a cessé: après tout, les feuilles d'or ne bougent plus, ce qui indique que les charges ne changent plus.
Il s'ensuit que l'influence électrique totale, celle de toutes les charges maintenant en présence, soit en A , C et D , doit être nulle dans le conducteur. La somme des influences électriques de chaque charge, induite ou non, doit donner zéro puisque le fluide électrique n'est plus en mouvement.
Décharge partielle de BSi Canton touche le conducteur B avec son doigt en un point proche de D, il se trouve à le relier à la terre (le symbole de la terre est une série de lignes horizontales, d'autant plus courtes que plus basses, comme vu ci-contre): la charge de même signe que celle de A est alors éliminée par un mouvement du fluide électrique entre la région D du conducteur B et la terre. La feuille d'or attachée en D tombe, ce qui indique qu'il ne s'y trouve plus de charge électrique nette. Par contre la feuille d'or placée en C continue d'être repoussée.
La charge externe a donc, dans le cas où celle-ci est positive, repoussé vers la terre assez de fluide électrique pour que se forme en C une charge suffisamment grande pour contrer l'action de A dans le reste du conducteur. À ce moment, l'action électrique de toutes les charges en présence en C et en A est telle qu'il n'y a plus de déplacement de fluide électrique.
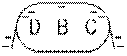B chargéIl enlève maintenant le doigt et éloigne finalement la charge A . Il remarque que les deux feuilles d'or sont repoussées, autant l'une que l'autre, mais moins qu'avant. Il touche avec sa feuille d'or placée sur un manche isolant n'importe quel point de la surface de B et il remarque à chaque fois que la feuille est attirée par la charge du corps A qu'il a placée plus loin: le corps B est maintenant chargé avec des charges de signe opposé à celui du corps extérieur (négativement, dans notre cas). Ce processus de charge est dit charge par influence.
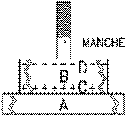Induction de l’électrophore
L'éloignement de la charge externe A a évidemment eu comme effet d'éliminer son influence sur le conducteur B . Le fluide électrique de B se répartit, somme toute, sur toute sa surface.
b) électrophore
Ce processus est utilisé un peu différemment en 1775 par le comte Allessandro Volta (1745-1827). Il fabrique une tarte de résine A et l'électrifie par frottement avec de la flanelle ou de la soie. Il attache au milieu d'un disque conducteur B un manche isolant. Il place maintenant le disque conducteur, manche vers le haut, sur la tarte de résine électrifiée: le disque ne touche réellement la tarte qu’en peu de points, et puisque les charges ne peuvent se déplacer sur la tarte, peu de celles-ci peuvent se retrouver sur le disque. La situation est donc telle que le disque est pratiquement juste au-dessus de la tarte de résine électrifié. Des charges de signe opposé à celles sur la résine apparaissent par influence sur la surface C du disque conducteur qui lui est la plus proche, et des charges égales mais de signe opposé sur la surface D qui lui est la plus éloignée.
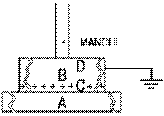Décharge partielleIl touche maintenant le disque conducteur sur s surface D: les charges sur la tarte de résine A entraînent alors un mouvement de fluide électrique, de la terre dans notre cas, qui entraîne la formation d'une charge en C telle que l'influence résultante des charges de A et C soit zéro. Il éloigne maintenant le disque conducteur B de la tarte de résine A qui a encore toute sa charge. Son disque chargé B est un électrophore, ce qui signifie: porteur de charge, qu'il a chargé par influence.
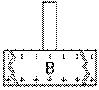Électrophore chargéc) champ électrique
Nous avons appelé la zone d'influence mesurable d'une charge électrique sur le fluide électrique d'un conducteur son champ électrique. Nous avons vu que l'action électrique varie en grandeur à l'intérieur de celle-ci; et que cette action entraîne un mouvement du fluide dans une direction et un sens précis, pour un point donné dans cette zone.
Comme dans cette zone la force de l'action sur le fluide électrique varie en grandeur et en direction, nous allons dire maintenant que le champ électrique, que nous notons E , est un vecteur dont la grandeur nous donne l'intensité de l'action sur le fluide électrique, et dont le sens nous indique le mouvement du fluide électrique.
Le champ électrique est donc l'influence électrique d'une charge ou d'un ensemble de charges; et celle-ci diffère d'ordinaire d'un point à l'autre. Remarquons que ce concept d'influence électrique en un point ne demande même pas qu'il y ait physiquement un conducteur en ce point pour en ressentir l'effet: l'influence existe, indépendamment de lui, mais ne peut tout simplement pas être mesurée.
1.8 Charges placées dans des gobelets
a) cas d’un gobelet isolant
La force électrique de répulsion entre des charges de même type est mise en évidence de façon dramatique par une expérience fort simple: la surface interne d'un gobelet de verre est électrifiée par frottement. Des boules de liège, un isolant léger, sont placées dans le gobelet; aussitôt après avoir touché la paroi interne électrisée du verre, elles sont comme projetées de la paroi et s'entrechoquent violemment. Ce mouvement s'explique simplement: chaque boule acquiert une charge de même type lors de son contact avec la surface électrifiée; et donc toutes se repoussent les unes les autres en plus de fuir la surface interne électrisée du gobelet.
b) cas d’un gobelet conducteur
Mais voilà que Franklin remarque en 1766 que des boules de liège ne se comportent pas ainsi lorsque placées dans un gobelet de métal électrisé de la même façon. Il doit donc en conclure que celles-ci ne doivent pas avoir été électrisées par attouchement avec la paroi interne du gobelet conducteur.
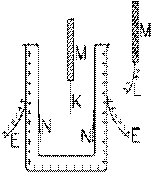Gobelet conducteur
chargéc) charges et champs d’un gobelet conducteur
Il demande à son ami Joseph Priestley (1733-1804) d'examiner ce phénomène plus à fond. Priestley place des petites feuilles d'or sur les parois interne et externe de son gobelet conducteur. Il l'électrifie ensuite à l'aide de sa machine électrostatique et constate que les feuilles d'or externes E s'éloignent de la paroi du gobelet mais pas les feuilles d'or internes N. Il conclut donc qu'il n'y a pas de charge sur la paroi interne du gobelet: voilà pourquoi les petites boules de liège de Franklin n'ont pas été électrisées. Il amène une petite feuille d'or placée sur un manche isolant M proche de la paroi interne du conducteur: la feuille K n'est ni attirée, ni repoussée: elle ne subit aucune force, contrairement au cas où il approche une feuille L de la paroi externe. Non seulement la charge est nulle sur la paroi interne du gobelet, mais la force électrique est nulle dans la région à l'intérieur du gobelet conducteur.
Or il avait été montré qu'un corps creux n'attire pas un corps qui est placé en son intérieur si leur force d'attraction (de la gravitation) est inversement proportionnelle au carré de la distance qui sépare chaque élément de ces corps. Fort de ses résultats, Priestley conclut, en 1766, que la force électrique doit être de cette forme, et donc que la force électrique entre deux éléments électriques doit être inversement proportionnelle au carré de la distance qui les sépare.
1.9 La balance de torsion de Coulomb
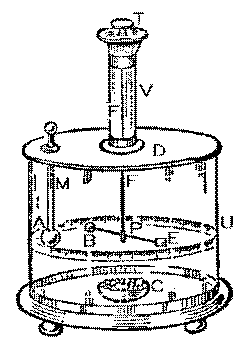Balance de torsion de Coulomb
Charles Augustin de Coulomb (1736-1806) découvre, en 1784, les lois de la torsion de fils. Il trouve que le moment de force Mt requis pour tordre un fil donné d'un angle θ (la lettre grecque thêta minuscule) est proportionnel à cet angle:
Il trouve également comment la constante de proportionnalité χ (la lettre grecque chi minuscule), dite constante de torsion, dépend de la longueur du fil utilisé, de son diamètre et du matériau lui-même.
Il est alors en mesure de mettre au point en 1785 une balance de torsion très sensible. John Michell (1724-1793) en avait déjà fabriqué une en 1750 mais celle de Coulomb est supérieure. Elle consiste en un long fil mince d'argent F qui porte en son extrémité inférieure une paille P recouverte de cire. La paille tourne dans un tube de verre de grand diamètre U où se trouvent indiquées les positions angulaires. La paille est fixée de telle sorte que son centre coïncide avec l'axe du fil d'argent. À une extrémité de la paille est fixée une petite boule B de moelle de sureau. À l'autre extrémité, un petit morceau de papier E , afin d'équilibrer le montage. Le tube de verre de grand diamètre est recouvert par un disque de verre D muni de deux trous. Le fil d'argent est fixé à une tête de torsion rotative T placée au sommet d'un petit tube de verre V placé au-dessus de l'autre et de même axe et qui donc se trouve au-dessus d'un des deux trous du couvercle du tube D . L'autre trou permet d'insérer un manche isolant M à l'extrémité duquel se trouve une deuxième petite boule de moelle de sureau A . Il place de la chaux C dans un bocal afin de garder sec l'air à l'intérieur, afin d'éviter la perte de charge due à l'humidité, phénomène déjà connu par Gilbert.
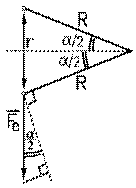
Il agence son système pour que les deux boules de sureau A et B se touchent quand il n'y a pas de moment de torsion sur le fil. L'angle de torsion θ est donc nul. Il charge maintenant les deux boules de sureau avec des charges de même signe: il trouve que la paille tourne d'un certain angle α (la lettre grecque alpha minuscule) vu la force de répulsion entre les boules électrisées. Il peut mesurer la distance r entre les deux boules de sureau comme il connaît le rayon R , entre l'axe du fil et la boule de sureau fixée sur la paille, et l'angle α duquel la paille a tourné.
Il sait que la force électrique entre les deux boules est selon la droite qui les réunit. Or celle-ci fait un angle α / 2 avec la perpendiculaire au rayon R . Or le moment d'une force, électrique ici, est donnée par le produit de la distance entre son point d'application et l'axe de rotation, soit ici R , par sa composante perpendiculaire à cette dernière. Il s'ensuit que le moment de force électrique est donné par
Si le système est au repos, il faut que le moment de force électrique Me soit compensé exactement par le moment de force de torsion Mt donné par notre équation (1.9.1).
Dans un premier cas, il trouve que le moment de force électrique est compensé par le moment de torsion lorsque la paille a tourné d'un angle α de 36°. Il s'ensuit que le fil a été tordu par un angle de 36° également.
Il force maintenant la paille à ne plus faire qu'un angle de 18° par rapport à sa position originale; ce qui demande de tordre le fil en son sommet d'un angle β (la lettre grecque bêta minuscule) de 126°. L'angle de torsion total θ est la somme de l'angle de rotation de la paille α et de l'angle de torsion supplémentaire β , soit ici de 18° plus 126°, ce qui donne 144°.
Il force finalement la paille à ne plus faire qu'un angle de 8,5° par rapport à sa position originale; ce qui demande de tordre le fil en son sommet d'un angle β de 567°. L'angle de torsion total θ est la somme de l'angle de rotation de la paille α et de l'angle de torsion supplémentaire β , soit ici de 8,5° plus 567°, ce qui donne presque 576°.
Il remarque que, lorsque l'angle de rotation α est deux fois plus faible, (et donc que la distance entre les deux boules est pratiquement deux fois plus faible), l'angle de torsion θ requis pour avoir équilibre est 4 fois plus grand (et donc la force électrique entre les deux boules est pratiquement 4 fois plus grande). Et que la même chose se produit presque lorsqu'il coupe l'angle de rotation à nouveau en quadruplant l'angle de torsion θ à nouveau (mais l'angle est de 8,5° au lieu de 9°). Dans ce dernier cas, la distance entre les boules est plutôt faible et donc comparable aux dimensions des boules chargées. Leur charge n'apparaît donc pas comme concentrée seulement en un point. S'il suppose que leur charge est comme concentrée en leurs centres, la distance apparaît comme un angle de près de 9°.
1.10 La loi de Coulomb pour les charges ponctuelles
Coulomb conclut donc de ces résultats que la force électrique va comme l'inverse du carré de la distance entre ses deux boules de sureau lorsque leurs charges apparaissent comme concentrées en un point. Dans pareil cas, leurs charges sont dites ponctuelles puisque leur rayon est petit comparé à leur distance de séparation.
Il fait la même expérience avec des boules de sureau chargées avec des électrifications de signes opposés, et trouve que leur force électrique, d'attraction cette fois, va également comme l'inverse de leur distance.
Il remarque que sa machine électrostatique lui fournit la même charge chaque fois comme il obtient les mêmes déviations. Il place maintenant une charge double sur une de ses deux boules de sureau: il obtient une force électrique deux fois plus grande; et cela, qu'il charge ainsi la boule fixe ou celle qui est montée sur la paille. Il s'ensuit que la force électrique est proportionnelle à chaque charge.
La force électrique est, comme toute force, un vecteur, soit une quantité qui a un sens, une direction donnée, en plus d'une grandeur. Une force s'exerce sur un corps. Or nous en avons deux: nos deux boules de sureau électrifiées. La troisième loi de sir Isaac Newton (action-réaction) stipule que les deux boules subissent des forces électriques de grandeurs égales mais de sens opposés. Mais Coulomb ne fait qu'examiner la force exercée sur la boule de sureau électrifiée attachée à la paille: c'est elle qui subit la force électrique qu'il cherche à mesurer. Et l'autre boule de sureau agit dans ce cas comme celle qui cause en quelque sorte la force subie par l'autre. Nous pouvons donc dire ici que la charge mobile est la charge patient (celle qui subit la force électrique qui nous intéresse) alors que l'autre est la charge agent (celle qui la "cause").
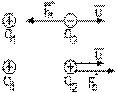
Définissons un vecteur dit vecteur unité noté dont la grandeur est l’unité 1 et qui a son point d'application à la charge patient mais dont le sens va de la charge agent vers la charge patient. Notons q la quantité d'électrification d'un corps, sa charge. Elle peut être, comme nous avons vu, ou positive, ou négative. Les relations que Coulomb a trouvées, en plus de celles déjà connues, à savoir que des charges de même signe se repoussent et que des charges de signes opposés s'attirent, nous permettent d'écrire la loi de Coulomb
où q1 est la charge agent et q2 est la charge patient, et ke est une constante. Cette dernière dépend évidemment des unités choisies. Dans le système d'unités M.K.S.A., l'unité de charge est le coulomb, noté C. Il est défini en 1881 en fonction de l'ampère, l'unité de courant électrique, que nous verrons plus tard. La constante ke fait alors 9,0 ⋅ 10 9 N m 2 / C 2 . Cette équation n'est valable que si les charges en question nous apparaissent comme ponctuelles.
1.11 La loi de Coulomb pour les pôles ponctuels
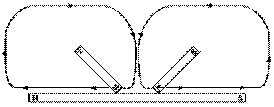Aimantation par double toucheCoulomb a employé le même principe pour mesurer la force magnétique entre deux pôles d'aimants. Michell avait déjà trouvé ce résultat en 1750 avec son montage moins précis. Coulomb fabrique de longues aiguilles aimantées en fer aigre avec la méthode de la double touche: deux aimants sont passés sur l'aiguille à aimanter, l'un présentant son pôle nord, l'autre son pôle sud, dans un mouvement allant du milieu de l'aiguille à son extrémité: cette méthode permet d'obtenir des aimants dont les pôles sont presqu'à leurs extrémités.
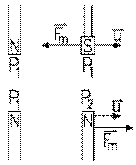
Une fois qu'il a bien repéré la position des pôles, il remplace la paille P par une de ces aiguilles, avec des pôles à chaque extrémité. Puis il remplace la tige M avec la boule de sureau A par une aiguille aimantée très longue, de telle sorte que seulement deux pôles, B et A , un pour chaque aimant, soient assez proches l'un de l'autre. Il mesure l'angle de torsion requis pour avoir équilibre ainsi que l'angle de rotation. Il trouve que la force magnétique va comme l'inverse du carré de la distance. Il renverse l'aiguille fixe de telle sorte que la force magnétique, de répulsive, devienne attractive: il trouve que les deux pôles d'un même aimant ont même puissance magnétique comme la force trouvée est identique en grandeur. Il remplace l'aiguille aimantée fixe par une autre: il trouve une force magnétique différente pour une distance d'éloignement identique; puis il place les deux aiguilles à la fois, de telle sorte que la puissance magnétique de deux pôles agissent sur celui de l'aiguille mobile: il trouve que la force magnétique est la somme des forces magnétiques trouvées préalablement, ce qui demande que la force magnétique soit proportionnelle à la puissance magnétique de chaque pôle.
Notons P la "puissance magnétique" d'un pôle. Celle-ci est dite positive s'il s'agit d'un pôle nord, et négative s'il s'agit d'un pôle sud. Les résultats de Coulomb sont alors
Cette dernière équation est similaire en tous points à celle des charges. Encore une fois, elle n'est valable que si les pôles apparaissent comme ponctuels.
Nous ne nous donnerons pas d'unités pour la puissance des pôles, ni ne chercherons à évaluer la constante km , puisque cela ne nous sera pas utile.
1.12 Champs et forces
a) champ électrique d’une charge ponctuelle
Nous avons dit plus haut que le champ électrique est l'influence électrique d'une charge ou d'un ensemble de charges; et qu'elle diffère d'ordinaire d'un point à l'autre. Voyons ce que ce concept implique dans le cas de la loi de Coulomb entre deux charges ponctuelles.
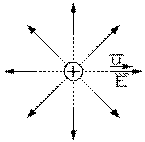Champ (charge positive)Nous avons remarqué qu'une façon de voir les choses est de dire qu'une charge (la charge agent) agit sur l'autre, la charge patient. Or il n'y a, dans notre équation (1.10.1), qu'une seule quantité qui dépende de la charge patient: la quantité q2 ; tout le reste est donc l'influence de la charge agent q1 là où se trouve la charge patient, donc le champ électrique
de la charge agent q1 en un point qui est à une distance r d’elle. Le vecteur unité doit être maintenant défini un peu différemment; son point d'application est le point où nous cherchons à évaluer le champ électrique, le point d'intérêt; et son sens est: de la charge agent vers ce même point d'intérêt.
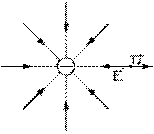Champ (charge négative)
Le vecteur s'éloigne toujours de la charge ponctuelle agent, que celle-ci soit positive ou négative. Le champ électrique d'une charge ponctuelle est donc radial. Le sens du champ est tel qu'il s'éloigne d'elle si elle est positive, puisque les vecteurs et sont alors de même sens, ou s'en approche si elle est négative, comme le vecteur est alors de sens opposé à puisque le signe de la charge agent est négatif.
b) relation champ et force électriques
Nos équations (1.10.1) et (1.12.1) nous permettent de trouver la relation entre la force électrique subie par une charge ponctuelle q et le champ électrique E qu'elle ressent là où elle se trouve:
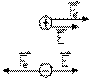
La force électrique subie par la charge ponctuelle q est donc de même sens que le champ E si celle-ci est positive; et de sens opposé au champ si elle est négative. Remarquons que cette relation ne suppose plus que le champ électrique qu'elle subit est dû à une charge elle-même ponctuelle; il peut être dû à n'importe quelle configuration de charges.
Notre équation (1.12.2) nous permet de trouver facilement les unités du champ électrique. Comme la force s'exprime en newton (noté N ) et la charge en coulomb (noté C ), le champ électrique s'exprime en newton par coulomb (noté N / C ).
Gilbert savait trouver la direction de ce que nous avons appelé le champ électrique avec son compas électrique, une petite aiguille faite d'un matériau conducteur et placée sur un pivot.
Le champ électrique local cause un mouvement du fluide électrique dans la petite aiguille conductrice, orientée au hasard, et ainsi induit des charges à ses extrémités: ces charges ressentent le champ électrique, ce qui entraîne une rotation de l'aiguille jusqu'à ce que sa charge positive induite pointe dans le sens du champ électrique qu'elle subit.
c) champ magnétique d’un pôle ponctuel
Tout comme nous avons défini le champ électrique comme l'influence électrique d'une charge, nous pouvons définir le champ magnétique comme l'influence magnétique d'un pôle, influence qui change d'ordinaire d'un point à l'autre. Voyons ce que ce concept implique dans le cas de la loi de Coulomb entre deux pôles ponctuels.
Ici encore nous pouvons dire qu'un pôle (le pôle agent) agit sur l'autre, le pôle patient. Il n'y a dans notre équation (1.11.1) qu'une seule quantité qui dépende du pôle patient: la quantité P2 ; tout le reste est donc l'influence du pôle agent P1 là où se trouve le pôle patient, donc son champ magnétique, que nous notons B :
Le vecteur unité est défini ici comme dans le cas du champ électrique: son sens va du pôle agent vers le point d'intérêt et son point d'application est ce dernier.
d) relation champ et force magnétiques
Nos équations (1.11.1) et (1.12.3) nous permettent de trouver la relation entre la force magnétique subie par un pôle ponctuel P et le champ magnétique B qu'il ressent là où il se trouve:
La force magnétique subie par le pôle P est donc de même sens que le champ B si celui-ci est positif (nord); et de sens opposé au champ s'il est négatif (sud). Aussi une boussole pointe-t-elle toujours son pôle nord dans le sens du champ magnétique local. Et, encore une fois, il n'est pas nécessaire que le champ magnétique subi par le pôle soit dû à un seul pôle, ou que celui-ci doive être considéré comme ponctuel.
1.13 Le pendule électrique
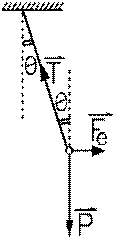Pendule électriqueUne boule de moelle de sureau électrisée, de masse m , placée à l'extrémité d'un fil de soie est utilisée depuis déjà plusieurs années comme façon de déterminer l'action d'une autre charge: si la charge agent cause une force horizontale sur la boule de sureau, de charge q, celle-ci va forcer le fil de soie à faire un angle θ avec la verticale, angle d'autant plus grand que la force électrique est grande. Sa mesure donne donc une indication de la grandeur de la force électrique horizontale ressentie par la charge placée sur la boule de moelle de sureau et donc, par l'équation (1.12.2), une indication de la grandeur du champ électrique qu'elle ressent. Cette masse chargée suspendue au bout d'un fil isolant est un pendule électrique.
Le poids P de la boule de moelle de sureau est strictement selon la verticale. Sous l'action de la force électrique Fe subie par la charge q de la boule, le fil de soie fait un angle θ . La tension T dans le fil de soie fait donc ce même angle avec la verticale.
Comme le pendule est en équilibre, la somme des forces qui agissent sur la boule de moelle de sureau est nulle. Ce qui nécessite que, selon l'horizontale, la force électrique (toute selon l'horizontale) soit compensée par la composante, selon l'horizontale, de la tension
et que, selon la verticale, la composante selon la verticale de la tension compense le poids de la boule de moelle de sureau
Il s'ensuit que le champ électrique est proportionnel à la tangente de l'angle que fait le fil de soie avec la verticale
Évidemment ce pendule est d'autant plus sensible que la masse suspendue est faible, et que sa charge est grande.
1.14 Champ résultant
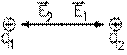
Si la boule de moelle de sureau d'un pendule électrique est placée à mi-chemin entre deux autres boules de sureau, chargées avec des charges égales q1 et q2 de même signe, elle n'est attirée ni vers l'une, ni vers l'autre. Or le champ électrique de chacune des deux boules, pris indépendamment, E1 et E2 , donné par notre équation (1.12.1), est égal à l'autre mais de sens opposé
Comme le fil de soie auquel est attachée la boule de sureau chargée reste verticale, il faut que la force électrique qu'elle ressent soit nulle, et donc que le champ électrique résultant dû aux deux charges à la fois ER qu'elle subit le soit également. Ce qui est le cas si celui-ci est donné par
puisque la somme des champs de chacun pris indépendamment donne zéro. Le champ résultant est donc vraiment donné par la somme vectorielle des champs électriques de chaque charge en supposant que cette charge est seule en présence. Cette façon de faire, dite principe de superposition, s’applique donc dans ce cas.
La force électrique due à deux charges sur une troisième q3 placée en ce point doit donc être donnée par notre équation (1.12.2) avec le champ résultant ER donné par notre équation (1.13.2) comme champ électrique local.
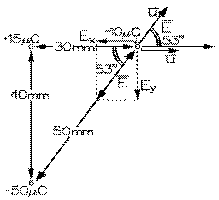
Considérons le cas de trois charges ponctuelles, de + 15 μC, - 50 μC et de - 10 μC telles que placées sur le diagramme ci-contre. Cherchons le champ électrique résultant là où se trouve la charge de - 10 μC. Nous remarquons que le vecteur unité de la première charge est vers la droite; et que, comme cette charge est positive, son vecteur champ électrique est lui-aussi vers la droite. Sa grandeur est donnée par notre équation (1.12.1) avec la valeur de la constante déjà connue. La charge en question est de 15⋅10-6 C et la distance est de 30⋅10-3 m. Ce qui donne ici 1,5⋅108 N/C. Remarquons bien que un microcoulomb est un millionième de coulomb.
Remarquons que le vecteur unité de la charge de - 50 μC fait un angle de 53° au nord de l'est. Comme la charge est négative, son vecteur champ au point d'intérêt fait un angle de 53° au sud de l'ouest. Sa grandeur est donnée par notre équation (1.12.1) avec la valeur de la charge en question de 50⋅10-6 C et la distance, de 50⋅10-3 m. Ce qui donne ici 1,8⋅108 N/C. Remarquons bien que nous avons considéré la charge en valeur absolue; ceci parce que nous avons déjà tenu compte de l'effet de son signe sur le sens du vecteur champ.
Décomposons ce dernier vecteur selon les axes X et Y. L'angle qu'il fait est de 233° (soit 180° + 53°) par rapport à l'axe X. Sa composante selon X est donnée alors par sa grandeur fois le cosinus de cet angle, soit - 1,08⋅108 N/C; sa composante selon Y, par sa grandeur fois le sinus de cet angle, soit - 1,44⋅108 N/C.
Nous avons maintenant à tenir compte de deux vecteurs champs selon l'axe X: la composante juste trouvée et le champ de la première charge. Ces deux champs sont de sens opposés. La résultante est + 0,42⋅108 N/C (1,50⋅108 - 1,08⋅108). Nous n'avons qu'une composante selon Y, celle de -1,44⋅108 N/C. Le vecteur résultant est donné par l'hypoténuse. Nous obtenons donc, à l'aide du théorème de Pythagore, une valeur de 1,50⋅108 N/C. L'angle θ que fait ce vecteur champ résultant avec l'axe des X est tel que sa tangente est donnée par le rapport de sa valeur selon Y, soit - 1,44⋅108, et de + 0,42⋅108, soit de - 3,43. L'angle correspondant à cette tangente est de 286,3°.
La force subie par la charge de - 10 μC en ce point est donnée par notre équation (1.12.2). Son sens est opposé à celui du champ électrique comme le signe de sa charge est négatif: elle fait donc un angle de 106,3°. Sa grandeur est donnée par le produit de sa charge par le champ, ce qui donne 1,5⋅103 N.
1.15 Les autres travaux de Coulomb
Coulomb se sert de sa balance de torsion pour mesurer la grandeur de charges. Ceci, en mesurant, pour une charge placée sur la boule de sureau mobile B donnée, l'angle de torsion θ requis pour la maintenir à une distance donnée de l'autre boule A qui a reçu la charge à mesurer.
Il invente ce qu'il appelle le plan d'épreuve: c'est une petite surface plane métallique flexible placée sur un manche isolant. Il remarque que, s'il appose sur une surface chargée son plan d'épreuve, celui-ci recueille une certaine charge. Il peut maintenant la transporter, une fois prélevée de l'objet électrique étudié, et la placer comme charge A dans sa balance de torsion. Et ainsi, la mesurer.
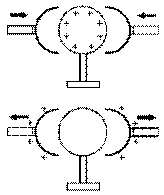Hémisphères de CoulombIl décide de vérifier que la charge d'une sphère métallique est bien superficielle. Pour ce faire, il construit deux hémisphères métalliques, attachés chacun à un manche isolant, qu'il peut placer sur la sphère isolée de telle sorte qu'ils la recouvrent parfaitement en la touchant en tout point.
Il débute en chargeant sa sphère à l'aide de sa machine électrostatique. Il vérifie, à l'aide de son plan d'épreuve, que la sphère métallique isolée est bien chargée: il trouve l'angle de torsion requis pour maintenir A et B à une distance choisie. Il place ses deux hémisphères en contact complet avec la sphère. Ce sont leurs surfaces externes qui constituent la surface externe de l'ensemble conducteur. Il enlève maintenant les deux hémisphères. Il touche la sphère conductrice avec son plan d'épreuve et le place dans sa balance de torsion. Il remarque que ce dernier ne porte pas de charge. Il touche la surface externe de ses hémisphères avec son plan d'épreuve: il remarque qu'il porte autant de charges que la première fois comme il doit tordre son fil du même angle pour maintenir la même distance. La charge est donc bien superficielle et dans le cas des conducteurs, et dans le cas des isolants.
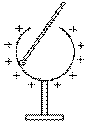
Il vérifie d'ailleurs que la surface interne d'une sphère creuse n'a pas de charge: il va toucher la surface interne d'une sphère creuse munie d'une petite ouverture en son sommet avec son plan d'épreuve; puis en mesure la charge avec sa balance de torsion électrique: il trouve que son plan d'épreuve ne porte aucune charge. Il n'en a pas collecté de la surface interne qu'il a touchée parce que celle-ci n'en porte pas.
Puisque la petite surface métallique A du plan d'épreuve est accolée momentanément sur la surface du corps chargé, il s'ensuit qu'elle devient en quelque sorte la surface externe locale de ce dernier et donc qu'elle ramasse toute la charge q trouvée sur la surface A du conducteur avec laquelle elle est en contact.
Le plan d'épreuve se trouve donc à collecter la charge q qui se trouvait sur sa surface A . Plus la charge collectée q est grande sur cette surface A , plus la charge par unité de surface σ , dite charge superficielle, notée à l'aide de la lettre grecque sigma minuscule, définie par ce rapport q sur A , est grande.
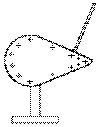
Il remarque que la densité superficielle de charge est la même partout sur une sphère, mais qu'elle varie si le corps est, par exemple, ellipsoïde: la densité superficielle augmente quand le rayon de courbure diminue. Plus le rayon de courbure est faible donc, plus les charges superficielles sont serrées. C'est donc à la pointe d'un conducteur que les charges vont aller se concentrer; il n'est alors guère étonnant que la pointe soit le point de départ ou d'arrivée du fluide électrique, comme l'avait montré Franklin.
Comment trouver le champ électrique résultant dû à une densité superficielle de charges? La loi de Coulomb, avons-nous vu, ne s'applique qu'à des charges ponctuelles. Nous ne pouvons donc pas l'utiliser sans modifications. Mais nous pouvons découper mentalement la surface chargée en un grand nombre de petites dalles chargées, chacune de surface infime, chacune portant une charge infime que nous notons dq (le d devant le q indique que la charge q est diablement petite). Cette petite dalle est, à toute fin pratique, ponctuelle. Son champ est donc celui d'une charge ponctuelle; mais comme la charge est infime, son champ dE l'est également. Notre équation (1.12.1) devient donc
Le champ résultant E est donné en faisant la somme des champs infimes de chaque charge infime constituant la charge superficielle totale. Cette somme, d'un nombre infini de termes infimes, est une intégrale, notée par un signe qui ressemble à la lettre s allongée
Nous n'allons pas chercher ici à calculer les champs électriques avec cette méthode, comme cela ne nous sera pas nécessaire par la suite.
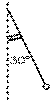
1.1 Quel est le champ électrique horizontal requis pour que la corde de 50 mm de longueur au bout de laquelle est placée une boule de 10 - 2 kg portant une charge de 5 μC fasse un angle de 30° avec la verticale?
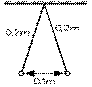
1.2 Deux boules légères, de masses égales, de charges + 0,5 μC et de + 0,4 μC, suspendues en un point commun par des fils de soie de 0,2 m chacun, sont à 0,1 m l'une de l'autre. Quelle est la masse de chacune?
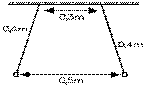
1.3 Deux boules légères, de masses égales, de charges + 0,2 μC et de + 0,4 μC, suspendues en des points d'une tige horizontale éloignés de 0,3 m par des fils de soie de 0,4 m chacun, sont à 0,5 m l'une de l'autre. Quelle est la masse de chacune?
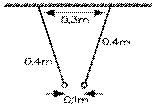
1.4 Deux boules légères, de masses égales, de charges + 1 μC et de - 2 μC, suspendues en des points d'une tige horizontale éloignés de 0,3 m par des fils de soie de 0,4 m chacun, sont à 0,1 m l'une de l'autre. Quelle est la masse de chacune?
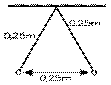
1.5 Deux petites boules, ayant une masse de 5⋅10 - 4 kg et de même charge, sont suspendues en un point commun par des fils de 0,25 m de longueur. Quelle est la charge de chacune si la distance entre elles est de 0,25 m?
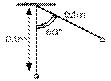
1.6 Une boule, dont la charge est de - 1 μC, est fixée à une distance de 0,1 m du sommet d'une corde verticale fixe, reliée à un crochet en son sommet. Une seconde, de même charge, est fixée à l'extrémité inférieure d'une corde de 0,1 m de longueur, reliée au même crochet. Cette corde fait alors un angle de 60° avec la première, toujours verticale.
a) Quelle est la tension dans la corde mobile?
b) Quelle est la masse de sa boule?
1.7 Trois charges, respectivement de + 5 μC, - 3 μC, + 4 μC, se trouvent à la suite sur une même droite. La distance entre les charges de + 5 μC et de - 3 μC est de 50 mm; celle entre les charges de - 3 μC et de + 4 μC, de 40 mm.
a) Quel est le vecteur champ électrique résultant là où sied la charge de + 4 μC?
b) Quel est le vecteur force électrique ressenti par la charge de - 3 μC?
1.8 Deux charges, l'une de + 50 μC, l'autre de - 128 μC, sont placées à 30 mm l'une de l'autre.
a) Où, dans leur voisinage, faut-il placer une charge de + 100 μC pour qu'elle ne subisse aucune force électrique?
b) Quelle force électrique subit alors la charge de + 50 μC?
1.9 Des charges de - 2 μC et de + 9 μC sont placées, sur une droite, à gauche et à droite d'une charge inconnue. La distance entre la charge inconnue et la charge négative est de 50 mm; celle entre la charge inconnue et la charge positive, de 100 mm. Or la charge de - 2 μC ne subit aucune force électrique nette.
a) Quels sont la grandeur et le signe de la charge inconnue?
b) Quel est le vecteur champ électrique là où sied la charge inconnue?
c) Quel est le vecteur force électrique subi par la charge inconnue?
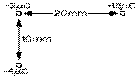
1.10 Une charge de + 16 μC est placée à 20 mm à droite d'une charge de - 2 μC et une charge de - 4 μC est placée à 10 mm en dessous, ces trois charges formant ainsi les sommets d'un triangle rectangle.
a) Quel est le vecteur champ électrique là où sied la charge de + 16 μC?
b) Quel est le vecteur champ électrique là où sied la charge de - 4 μC?
c) Quel est le vecteur force électrique exercé sur la charge de - 2 μC?
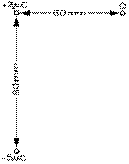
1.11 Une charge inconnue est placée à 60 mm à droite d'une charge de + 2 μC et une charge de - 5 μC est placée à 80 mm en dessous, ces trois charges formant ainsi les sommets d'un triangle rectangle, dont le troisième côté est de 100 mm. La force électrique subie alors par la charge de - 5 μC est strictement vers la gauche.
a) Quels sont la grandeur et le signe de la charge inconnue?
b) Quels sont la grandeur et le sens du champ électrique subi par la charge de + 2 μC?
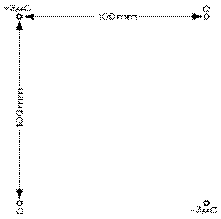
1.12 Une charge de + 2 μC occupe le coin supérieur gauche d'un carré de 100 mm de côté; une charge de - 3 μC, le coin inférieur droit. Les deux autres coins sont occupés par des charges identiques inconnues. Quels sont la grandeur et le signe de ces charges inconnues si le champ électrique subi par la charge de - 3 μC est nul?
1.13 Deux charges, chacune de +1 μC, sont placées, sur l'axe Y, à 30 mm du point centre (0 mm; 0 mm). L'une occupe donc les coordonnées (0 mm; +30 mm) et l'autre, les coordonnées (0 mm; -30 mm). Deux autres charges inconnues, de même valeur, sont placées, sur l'axe X, à 40 mm du point centre de telle sorte que leurs coordonnées sont (-40 mm; 0 mm) et (+40 mm; 0 mm) respectivement. Quelle doit être la valeur de ces charges inconnues identiques pour que celles-ci ne subissent aucune force électrique?