CHAPITRE HUIT

CIRCUITS À COURANT ALTERNATIF

            Nous allons dans ce chapitre examiner le cas de circuits électriques qui produisent ou sont soumis à un courant oscillatoire sinusoïdal. Ce courant sinusoïdal peut être dû à la décharge d'un condensateur dans une inductance. Mais il reste qu'il est le plus souvent dû à un générateur qui produit une tension de ce type, et donc, qui est différent des dynamos et magnétos que nous avons examinées dans notre chapitre six.

8.1 Le premier circuit oscillant

a) mise en marche

            Lorsque Henry examine, en 1842, les étincelles produites entre les extrémités des fils qui vont relier ensemble les armatures d'une bouteille de Leyde, et donc la décharger, il remarque non pas une seule étincelle, mais un train d'étincelles, partant l'une d'une électrode, et la suivante, de l'autre. Et ce, avec une intensité qui va en s'amenuisant. C'est donc que le courant causé par ce circuit oscille. C'est à ce circuit oscillant que lord Kelvin s'est intéressé d'abord en 1853, et non pas au problème de la charge et décharge d'un condensateur à travers une résistance.

            Débutons avec un condensateur, la bouteille de Leyde de Henry, portant sur ses armatures une charge Q₀ , aux bornes duquel nous branchons une inductance: les fils et l'air conducteur entre leurs extrémités. Ceux-ci forment une inductance car tout élément où un courant cause un champ magnétique en est une.

b) énergies magnétique, électrique et totale

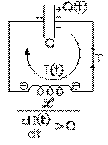
            Un courant I (t) circule donc dans cette inductance, de l'armature positive du condensateur à l'autre. Le courant, de nul au départ, augmente dans le temps: l'inductance réagit, selon la loi de Lenz, pour s'opposer à l'établissement de ce courant: ses polarités sont celles d'une force contre-électromotrice (soit celle d'une résistance): l'énergie électrique U_e , donnée par notre équation (7.9.4), emmagasinée dans le condensateur, le quitte donc, et migre dans l'inductance sous forme d'énergie magnétique U_m , donnée par notre équation (7.9.9).

            Le principe de conservation de l'énergie, mis de l'avant par Helmholtz quelque temps auparavant, implique ici que la somme de ces deux formes d'énergies, l'énergie totale ℰ

doit être constante. Initialement, toute l'énergie ℰ est emmagasinée sous forme d'énergie électrique

dans le diélectrique du condensateur. Puis, une partie sans cesse grandissante est emmagasinée dans le champ magnétique de l'inductance puisque le courant grandit. Elle est entièrement emmagasinée dans le champ magnétique

quand la charge du condensateur devient nulle, moment auquel le courant dans l'inductance est maximal I₀ . Le principe de conservation de l'énergie implique une relation entre le courant maximal I₀ et la charge initiale (et également maximale) Q₀

puisque les termes de droite des équations (8.1.3) et (8.1.2) correspondent tous deux à l'énergie totale ℰ .

c) charge et courant obtenus

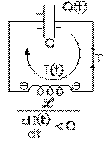
            Les armatures du condensateur reçoivent maintenant des charges, mais de signes opposés au cas initial. Le condensateur recommence donc à emmagasiner de l'énergie électrique, énergie qui provient du champ magnétique de l'inductance qui agit maintenant comme une force électromotrice. Nous avons donc une situation de flux et de reflux, le courant allant d'abord dans un sens dans l'inductance, puis dans l'autre. Le courant est donc oscillatoire, ainsi que la charge des armatures du condensateur. Cette dernière peut donc être donnée par

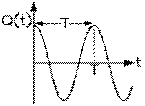
sa valeur initiale Q₀ fois la fonction oscillatoire cosinus, choisie puisqu'elle donne l'unité au temps zéro, et où la vitesse angulaire, dite également fréquence angulaire, ω est une constante. Ce terme est la rapidité avec laquelle la fonction revient à sa situation originale. Le temps T requis pour que la fonction revienne, de nouveau, à la même valeur, est sa période. Sa fréquence f est l'inverse de la période. La fonction cosinus étant récursive à tous les 2 π radians, il s'ensuit que

vitesse angulaire, période et fréquence sont reliées.

            Le courant est, avons-nous vu à plusieurs reprises, la dérivée de la charge dans le temps; ce qui est, dans le cas où la charge est donnée par notre équation (8.1.5),

le négatif de la valeur maximale Q₀ fois ω fois la fonction oscillatoire sinus. Puisque la valeur maximale de la fonction sinus (tout comme celle de la fonction cosinus d'ailleurs) est l'unité, le terme entre le signe négatif et la fonction sinus est la grandeur maximale I₀ que peut valoir le courant. Ce terme est dit son amplitude. Notre dernière équation peut donc se réécrire

d) fréquence d’oscillation

            Notre équation d'évolution de la charge dans le temps (8.1.5) implique, d'après notre dernière équation, que la fréquence angulaire ω est le rapport des amplitudes du courant I₀ et de la charge Q₀

rapport, trouvé à notre équation (8.1.4). La fréquence f du train d'étincelles est trouvée

avec notre dernière équation et (8.1.6).

e) énergies

            Nous pouvons vérifier que notre équation de l'évolution de la charge dans le temps (8.1.5) est bien une solution de notre équation initiale (8.1.1)

après avoir fait appel aux équations (8.1.2), (8.1.8), et (8.1.3), puisque la somme des carrés des fonctions cosinus et sinus est bien l'unité par le théorème de Pythagore. L'énergie totale passe donc d'électrique à magnétique, et vice-versa, avec une fréquence qui dépend de la valeur de l'inductance et de la capacité du circuit en question. Cette fréquence f est la fréquence naturelle d'oscillation du circuit.

f) énergie dissipée par la résistance

            Il reste que le circuit est résistif, et donc que l'énergie totale emmagasinée ℰ est dissipée par effet Joule. Supposons cette dissipation suffisamment lente pour que l'amplitude du courant puisse être considérée constante sur la durée de chaque période. L'évolution, dans le temps, de la puissance dissipée durant une période est alors

donnée par la loi de Joule avec notre équation (8.1.8) pour le courant.

            La puissance moyenne P_m , dissipée durant la période T , est donnée par le rapport de

la valeur absolue de l'énergie ∣Δℰ∣ dissipée dans ce temps, divisée par cet intervalle.

            L'énergie dissipée ∣Δℰ∣ sur une période T est l'intégrale de la puissance instantanée P (t) donnée par notre équation (8.1.12)

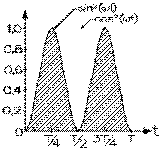
sur cet intervalle, notre période T .

            Le calcul de cette énergie dissipée ∣Δℰ∣ sur une période T revient à trouver la surface sous la courbe en question, dont le croquis est donné ci-contre. Traçons-y une droite parallèle à l'axe des temps, de hauteur égale à la moitié de la hauteur maximale de notre courbe. La région 1 , qui se trouve sous la courbe mais au-dessus de cette droite, peut être renversée pour remplir la région 2 qui, elle, n'est pas sous la courbe, mais entre cette droite et la courbe. La région 3 peut, elle, remplir la région 4 et la région 5 , la région 6 . Il s'ensuit que toute région, sous la courbe originale qui est au-dessus de notre droite à mi-hauteur, se trouve à avoir rempli toute région de la courbe originale qui n'était pas sous celle-ci. L'énergie dissipée ∣Δℰ∣ sur une période T est donc donnée par la surface d'un rectangle

dont la "hauteur" est la moitié de la puissance maximale R I₀² et dont la base est la période T.

g) puissance moyenne dissipée

            La puissance moyenne P_m n'est donc rien d'autre que

la moitié de la puissance instantanée maximale, puissance produite au moment où le courant est maximal.

            De plus, nous remarquons que la moyenne, sur une période, de la fonction sinus carré

est de une demie en comparant les équations (8.1.14) et (8.1.15).

h) variation du courant pour un circuit oscillant faiblement résistif

            L'énergie totale ℰ du circuit oscillant est donnée par notre équation (8.1.3). Celle-ci décroît avec le temps. La variation temporelle de l'énergie totale est donc négative. Le taux de perte de celle-ci dans le temps est donné par la puissance moyenne P_m dissipée par la résistance. Mais cette dernière est une quantité positive. Il faut donc placer un signe négatif devant la variation temporelle de l'énergie totale

pour que les deux membres de notre équation soient positifs.

            Une fois la dérivée effectuée, notre dernière équation devient

à l'aide de l'équation (8.1.16). Isoler la variation de l'amplitude du courant dans le temps

après simplification montre que celle-ci est proportionnelle à elle-même. Sa solution est donc

la fonction exponentielle. L'amplitude décroît d'autant plus vite que la résistance est grande puisque la puissance dissipée lui est proportionnelle, pour un courant donné; et d'autant moins vite que l'inductance est grande, puisque celle-ci a emmagasiné d'autant plus d'énergie que celle-ci est grande, encore une fois, pour ce même courant.

            L'équation de l'évolution du courant en fonction du temps est donc, dans le cas du circuit oscillant où l'énergie n'est dissipée que très lentement, donnée par

nos équations (8.1.21), (8.1.8) et (8.1.9).

            Berend Wilhelm Feddersen (1832-1918) mesure la fréquence d'oscillation de circuits semblables en 1857, à l'aide d'un miroir tournant, et montre alors que la fréquence double quand la capacité devient quatre fois plus faible; et que la fréquence double quand l'inductance devient quatre fois plus faible, comme l'affirme notre équation (8.1.10).

8.2 Génération de courant alternatif

            Nous avons vu dans notre section précédente que le courant sinusoïdal produit des étincelles, tout comme le courant continu. Il peut alimenter les lampes à arc que nous avons vues dans notre chapitre cinq. Il n'y a donc aucune raison, à prime abord, pour rechercher une tension aussi continue que possible pour nos générateurs, comme nous l'avons fait dans notre chapitre six.

a) alternateurs

            Aussi sont développés en même temps que nos magnétos et dynamos des générateurs alternatifs, également dits, depuis 1893, alternateurs. Ceux-ci ne produisent pas une tension, et donc un courant, purement sinusoïdaux, mais qui alternent de façon périodique. Il est montré, aussitôt l'ampoule électrique mise au point, que ceux-ci peuvent l'alimenter tout aussi bien que les dynamo et magnéto. C'est avec un générateur alternatif, fabriqué par Siemens, que des lampes à incandescence éclairent le tout nouveau théâtre Savoy de Londres, bâti en 1881 par la compagnie D'Oyly Carte.

            Le baron Joseph Fourier (1768-1830) avait découvert en 1812 que toute fonction périodique peut être écrite en termes d'une série de fonctions sinus et cosinus dont les arguments sont des multiples entiers de l'argument du premier terme. La valeur, obtenue à un moment, de tout courant alternatif produit par un générateur alternatif, est obtenue à nouveau une période plus tard. La fréquence angulaire correspondant à cette période est donnée par notre équation (8.1.6). Il s'ensuit, selon Fourier, que la fonction sinus du premier terme de la série a comme argument cette fréquence angulaire fois le temps correspondant au moment qui nous intéresse. Les autres fonctions sinus de la série vont avoir des fréquences angulaires double, triple, quadruple, et ainsi de suite, de la fréquence angulaire initiale.

Le développement de réseaux électriques alternatifs débute en 1882: une ligne de transmission alternative, sous une tension de 2 kV, est alors installée à Munich sur une longueur de 50 km; deux alternateurs Siemens de 250 kW chacun fournissant une tension de 2 kV sont installés à Londres. Alexander Siemens invente le moteur alternatif à vitesse variable en 1884. George Westinghouse (1846-1914) installe des alternateurs Siemens à Pittsburg en 1885. Sa compagnie développe son propre alternateur en 1886. Sebastian Ziani de Ferranti (1864-1930) installe à Londres deux alternateurs de son invention, de 400 kW chacun, à une tension de 2,4 kV, également en 1886. En 1889, des alternateurs entrent en production à Calgary et à Ottawa. Les alternateurs de la centrale hydro-électrique de Chambly de la Royal Electric Company alimentent des quartiers de Montréal en 1893. Et en 1894 dix alternateurs sont installés aux chutes Niagara.

L'analyse (théorique) détaillée des phénomènes reliés au caractère sinusoïdal du courant alternatif ne vient que dix ans après le début des réseaux alternatifs, avec la publication, en 1892, des Electrical Papers de Heaviside et, en 1893, du Theory and Calculation of Alternating Current Phenomena de Charles Proteus Steinmetz (1865-1932). Ces analyses permettent alors de comprendre un certain nombre de phénomènes observés mais non compris correctement, et de montrer l'utilité de rechercher la production d'un courant alternatif qui soit purement sinusoïdal, c'est-à-dire un courant où l'amplitude de chacun des autres termes de la série de Fourier est nulle.

b) le téléphone

            Un autre cas de production du courant alternatif est le téléphone. Philipp Reis découvre en 1861 qu'une membrane conique sur le col de laquelle est roulée une bobine de fil placée dans le champ magnétique d'un aimant permanent, va, en vibrant, faire bouger la bobine dans le champ magnétique et ainsi causer une force électromotrice induite selon la loi de Faraday à la fréquence du mouvement de la membrane. Si les fils, reliés à la bobine vibrant alors, dite émetteur, sont reliés à une autre bobine identique, dite récepteur, elle aussi placée dans le champ magnétique d'un aimant permanent sur le col d'une membrane conique, le courant qui y circule va causer une force magnétique qui va entraîner la membrane dans le même mouvement de va-et-vient que la membrane originale. Et donc, le mouvement que subit la première membrane (l'émetteur) est copié par la seconde (le récepteur). Il appelle téléphone cet appareil qui reproduit ainsi des sons à distance mais ne le développe pas.

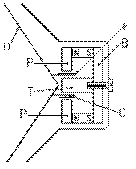
            Remarquons que le récepteur en question est l'ancêtre du haut-parleur de nos systèmes de son. L'aimant permanent est, dans ce dernier cas, tubulaire. La partie de droite de l'aimant sur notre croquis, son pôle sud, est en contact avec un disque de fer doux B lui-même en contact avec une tige T également en fer doux. La partie gauche de l'aimant, son pôle nord, est en contact avec un anneau épais de fer doux P . Le col C de la membrane se trouve dans l'entrefer créé entre les pièces de fer doux P et T magnétisées de telle sorte que le champ magnétique est de la pièce P vers la pièce T . Chaque spire de la bobine de fil F va donc subir une force magnétique quand un courant va y circuler, force qui sera vers la gauche ou vers la droite selon le sens du courant. La membrane, le diaphragme D ,va donc aller ou venir à la fréquence du courant, produisant ainsi un son identique à celui de l'émetteur.

            Ignorant le travail de Reis, Alexander Graham Bell (1847-1922) examine le travail de Helmholtz, qui avait montré que la voix est due à la superposition d'ondes sinusoïdales, et arrive en 1875 aux mêmes résultats que Reis: le son produit est très faible.

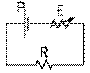
            Bell avait remarqué préalablement que, si le courant du télégraphe, coupé et réintroduit plusieurs centaines de fois par seconde, alimente son récepteur R , celui-ci vibre plusieurs centaines de fois par seconde et le son correspondant est alors obtenu. Il invente alors en 1876 un émetteur E dont la résistance varie selon la pression que subit un diaphragme sous l'action de la voix. La résistance, variable dans le temps, joue, en quelque sorte, le rôle de la clef de télégraphe, modulant le courant fourni par la pile P selon la résistance totale du circuit, résistance constituée surtout par cette résistance variable E .

            Cette dernière résistance est une courte colonne constituée d'une solution d'acide très diluée entre un disque métallique et une tige métallique attachée au diaphragme. La résistance de la solution, dont la résistivité est grande, varie selon sa longueur, déterminée par la position du diaphragme mobile, qui varie selon la pression de l'air causée par l'onde sonore.

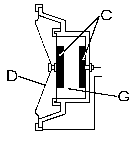
            David Edward Hughes (1831-1900) remarque en 1878 que la résistance de granules G de carbone placés librement dans un contenant, entre deux électrodes conductrices C , varie de façon importante selon la pression que l'ensemble subit, sous l'action du mouvement du diaphragme D , puisque les granules G sont en plus ou moins bon contact selon la pression. Cette résistance variable, solide, est beaucoup plus commode que celle, liquide, trouvée par Bell. Aussi la remplace-t-elle rapidement. Hugues baptise cette résistance, qui varie selon la pression de la voix exercée contre un des deux disques conducteurs, microphone, puisqu'elle permet d'amplifier de faibles sons une fois placée dans le circuit de la pile et du récepteur.

            Ce téléphone est produit commercialement à partir de 1877 et le premier échangeur téléphonique ouvre à New Haven, au Connecticut, en 1877. Le premier au Canada ouvre en 1878 à Hamilton; plus de 2000 téléphones sont bâtis au Canada entre 1879 et 1881. Le premier échangeur téléphonique voit le jour en Angleterre en 1879.

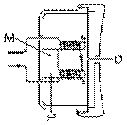
            Le récepteur comprend aujourd'hui un aimant permanent M et deux tiges de fer doux P autour desquelles sont roulées deux bobines de fil de telle sorte que leurs forces magnétomotrices s'additionnent. Le diaphragme D est placé proche des deux tiges de fer doux P et est fait d'un matériau ferromagnétique. Il est donc plus ou moins attiré, selon l'intensité du courant. Encore une fois, ses vibrations sont à la même fréquence que le courant: ce sont elles qui sont entendues.

8.3 Représentation du courant alternatif

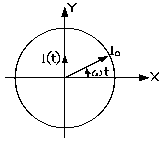
            Considérons un courant alternatif purement sinusoïdal

d'amplitude I₀ et de fréquence angulaire ω . Celui-ci peut être représenté à l'aide d'un vecteur tournant, vecteur inventé par Augustin Fresnel (1788-1827) en 1819. Le point d'application du vecteur tournant est l'origine des coordonnées. Sa grandeur, l'amplitude I₀ . L'angle qu'il fait alors avec l'axe des X est donné par l'argument ω t de la fonction sinus; et la valeur de I (t) , donnée par la projection du vecteur sur l'axe des Y . Nous avons donc une nouvelle représentation de la fonction sinus dont l'argument varie dans le temps. Le courant électrique, remarquons-nous, va et vient. La fonction sinus est, elle, ou positive, ou négative. Nous pouvons donc associer un sens du courant au cas positif, et l'autre, au cas négatif.

8.4 Effet sur une résistance

a) diagramme de phase tension-courant

            Puisque la loi d'Ohm donne la tension V_R (t) aux bornes d'une résistance R

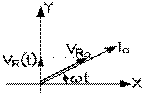
au moment où elle est parcourue par un courant I (t) , il s'ensuit que la tension aux bornes de la résistance est positive lorsque le courant qui la traverse l'est, et maximale en même temps que le courant qui la traverse. La même fonction sinus, avec le même argument, s'applique ici et au courant, et à la tension. Les vecteurs tournants de la tension et du courant sont donc en phase. Et leurs amplitudes sont également données par la loi d'Ohm

selon notre équation (8.4.1). L'amplitude d'une tension est également dite sa valeur de crête.

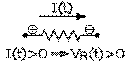
            Supposons que le courant circule vers la droite dans la résistance représentée ci-contre. Puisque le courant circule toujours, dans une résistance, de sa borne positive à sa borne négative, il s'ensuit que sa borne positive est alors à gauche, et à sa borne négative, à droite. Considérons positif le courant qui circule vers la droite; notre équation (8.4.1) exige alors que la tension aux bornes de la résistance soit également positive. Il s'ensuit qu'en courant alternatif, la tension aux bornes d'un élément est considérée positive si elle va du + au - dans le sens où le courant est considéré positif, et négative si elle va du - au + dans le même sens. Ce qui, évidemment, n'est pas en accord avec notre façon de faire des chapitres précédents.

b) valeurs efficaces

            La puissance dissipée, à un moment donné, par la résistance, est donnée par la loi de Joule, notre équation (8.1.12). La puissance moyenne, dissipée sur une période par une résistance parcourue par un courant sinusoïdal, est donnée par notre équation (8.1.16): celle-ci est proportionnelle à la résistance, et au carré de l'amplitude du courant alternatif. Mais cette équation diffère de la loi de Joule: le facteur une demie n'y apparaissait pas; il est dû au caractère sinusoïdal du courant.

            Il existe, évidemment, une valeur de courant continu, I , qui amènerait la résistance en question à la même consommation de puissance P que la puissance moyenne P_m

que le courant alternatif. Ce courant continu est donné, en l'isolant de notre équation précédente, par

l'amplitude du courant alternatif divisée par le radical de deux. Ce courant continu I fictif qui a, sur une résistance, le même effet sur une période que le courant sinusoïdal réel, est dit en français courant efficace. Diviser la valeur de crête de la tension par le même radical de deux

donne sa tension efficace V_R . Notre équation (8.4.2) devient, par la division de ses deux termes par radical deux,

la loi d'Ohm qui relie les valeurs efficaces de la tension aux bornes de la résistance et du courant qui la traverse grâce à nos équations (8.4.5 et (8.4.4).

c) mesure du courant alternatif par la balance de courant

            Nous avons vu à la section 3.9 comment mesurer le courant de façon absolue: avec la balance de courant d'Ampère. Le poids P requis pour contrecarrer la force magnétique F_m exercée par un fil rectiligne sur un autre de longueur L situé à une distance d du premier est donné par notre équation (3.9.1)

s'ils sont tous deux parcourus par le même courant continu I .

            Cette force magnétique va varier dans le temps comme

si le courant qui parcourt les deux fils est sinusoïdal. Le poids P requis pour contrecarrer cette force est alors égale à sa moyenne sur une période

qui devient

grâce à nos équations (8.1.17) et (8.4.4). Le poids requis P est donc relié au courant efficace I au carré. Il s'ensuit que la balance de courant mesure la valeur efficace du courant alternatif tout aussi bien que le courant continu.

d) mesure de la tension alternative par l’électromètre

            Nous avons également vu à la section 2.15 que la force mécanique F_a requise pour contrebalancer exactement la force électrique F_e entre deux disques sous des potentiels différents, donnée par notre équation (2.15.6), est proportionnelle

à la différence de potentiel V au carré. Cette force F_e se trouve à varier constamment

si la tension est sinusoïdale. La force mécanique F_a requise pour contrecarrer cette force est alors égale à la moyenne de cette dernière sur une période

qui devient

grâce à nos équations (8.1.17) et (8.4.5). La force mécanique est donc reliée à la tension efficace V au carré. Il s'ensuit que l'électromètre mesure la valeur efficace de la tension alternative tout aussi bien que la valeur continue.

e) mesures lues par des appareils de mesure en alternatif

            Tous les voltmètre et ampèremètre, qui lisent les tension et courant alternatifs donnent leurs valeurs efficaces, et non pas leurs valeurs de crête. Et ce sont elles, également, qui sont données dans les spécifications des éléments.

            La puissance consommée par une résistance en courant alternatif s'exprime donc, selon nos équations (8.4.3) et (8.4.6)

de la même façon que dans le cas du courant continu si les valeurs utilisées sont les valeurs efficaces. Celles qui sont toujours mesurées avec nos appareils.

Un circuit domestique est sous une tension alternative, fournie par Hydro-Québec, dite de 120 V. Cette valeur est une valeur efficace. La valeur de crête de cette tension est de presque 170 V selon l'équation (8.4.5). Un élément qui est dit consommer 600 W sous cette tension (efficace) de 120 V, supporte un courant (efficace) de 5 A selon l'équation (8.4.15), et donc un courant dont la valeur de crête est de presque 7,1A selon l'équation (8.4.4).

            Un alternateur peut donc allumer des ampoules électriques, faire chauffer des résistances tout comme une dynamo. Mais encore doit-il fournir une valeur de crête, supérieure par radical deux, à la valeur continue qui dissipe la même puissance sur une période, comme nous l'avons vu à l'équation (8.4.5).

8.5 Effet sur une inductance

a) diagramme de phase tension-courant

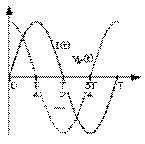
            La loi de Henry, avons-nous vu, nous permet de trouver la grandeur de la tension induite aux bornes d'une inductance V_ℒ (t)

selon la variation dans le temps du courant I (t) sinusoïdal qui y circule: celle-ci est proportionnelle au cosinus du même argument que le courant. Il reste que c'est la règle de Lenz qui détermine les polarités aux bornes de l'inductance.

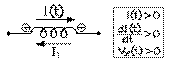           premier quart

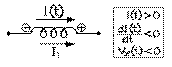          deuxième quart

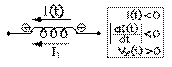
            Supposons que le sens positif du courant soit vers la droite. Puisque le courant est positif durant le premier quart de cycle, il s'ensuit qu'il circule alors vers la droite; puisqu'il croît alors, que l'inductance agit comme une force contre-électromotrice: elle cherche à faire circuler un courant induit dans le sens opposé, soit vers la gauche. Or le courant, causé par une force électromotrice, y circule du négatif au positif: donc la borne positive est à gauche, et la négative, à droite. La tension est alors positive puisqu'elle décroît dans le sens positif du courant.

            Durant le second quart de cycle, le courant est encore positif, et donc vers la droite. Mais il décroît alors: l'inductance agit alors comme une force électromotrice, cherchant à faire circuler un courant induit dans le même sens que le courant, soit vers la droite. Puisque le courant, causé par une force électromotrice, y circule du négatif au positif, il s'ensuit que sa borne négative est à gauche, et positive, à droite: sa tension est alors négative puisqu'elle croît dans le sens positif du courant.

           troisième quart

            Durant le troisième quart de cycle, le courant est négatif, et donc vers la gauche. Puisqu'il croît, l'inductance réagit comme une force contre-électromotrice, cherchant à maintenir le courant vers la droite: ses polarités demeurent alors: négative à gauche, positive à droite, et sa tension est encore négative puisque croissant dans le sens positif du courant.

          quatrième quart

            Durant le quatrième quart de cycle, le courant est négatif, et donc vers la gauche. Il décroît et donc l'inductance agit comme une force électromotrice, cherchant à maintenir le courant vers la gauche: ses polarités sont alors: positive à gauche et négative à droite. Sa tension est alors positive puisque décroissant dans le sens positif du courant.

            La tension est donc positive et négative exactement comme l'affirme notre équation (8.5.1).

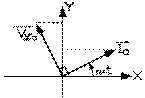
            Le terme devant la fonction cosinus de cette équation est l'amplitude (ou valeur de crête) de la tension aux bornes de l'inductance. La valeur de la fonction cosinus, pour un argument donné, est égale à celle de la fonction sinus si son argument est celui de la fonction cosinus, majoré de ( π / 2 ) . En quel cas la tension est dite être en avance sur le courant de ( π / 2 ) , comme le montre bien notre diagramme de Fresnel de ces vecteurs tournants.

b) réactance inductive

            Une fois notre équation (8.5.1) ainsi modifiée,

il est clair que la valeur de crête de la tension aux bornes de l'inductance est proportionnelle à celle du courant qui y circule. Ces deux termes, une fois divisés par le radical de deux, deviennent la tension efficace aux bornes de l'inductance et le courant efficace qui y circule. Le rapport entre, ou les valeurs de crête ou les valeurs efficaces, de la tension aux bornes sur le courant est la réactance de l'inductance X_ℒ

donnée, selon notre équation (8.5.2), par le produit de la fréquence angulaire par l'inductance elle-même. Les unités de la réactance sont, comme celle de la résistance, des ohms. Le rapport tension sur courant ne porte pas le nom de résistance, puisque ces deux quantités ne sont pas en phase dans le cas de l'inductance, mais bien déphasées de ( π / 2 ) : l'inductance agit, tantôt comme une force contre-électromotrice, tantôt comme une force électromotrice. Et c'est lorsque le courant instantané est nul que la tension instantanée est maximale, et quand le courant instantané est maximal que la tension instantanée est nulle. C'est au changement de courant instantané que réagit la tension instantanée. D'où le terme réactance, plutôt que résistance.

            La tension efficace est d'autant plus grande, pour un courant efficace donné, que celui-ci alterne rapidement, et que sa fréquence angulaire est grande. C'est pourquoi la réactance inductive est proportionnelle à la fréquence du courant alternatif.

c) puissance réactive absorbée

            L'inductance, absorbe, comme force contre-électromotrice, de l'énergie sous forme magnétique, énergie qu'elle remet ensuite comme force électromotrice. La puissance qu'elle reçoit est donnée par la loi de Joule, notre équation (5.6.6)

écrite à l'aide des équations (8.5.1), (8.5.2) et (8.3.1).

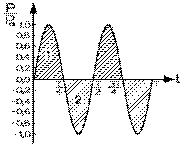
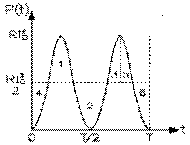
            La puissance moyenne P_m nette, reçue par l'inductance durant une période, est l'énergie nette reçue dans ce temps, divisée par cet intervalle. Or le calcul de cette énergie revient à trouver la surface sous la courbe en question, dont le croquis est donné ci-contre. La surface 1 correspondant à l'énergie reçue, emmagasinée dans le champ magnétique, est égale à la surface 2 correspondant à l'énergie remise: l'énergie nette, reçue sur une période, est nulle, et la puissance moyenne, également.

            La puissance moyenne, dissipée par une résistance, est donnée par le produit de la tension efficace à ses bornes par le courant efficace qui la traverse, selon notre équation (8.4.6). Le produit de la tension efficace aux bornes de l'inductance par le courant efficace qui la traverse n'est pas nul; mais ce n'est pas la puissance moyenne dissipée par l'inductance , vu que celle-ci ne consomme pas de puissance moyenne. Ce produit est la puissance réactive absorbée Π_b

par l'inductance (où la lettre grecque pi majuscule Π représente la puissance réactive) qui peut s'écrire de différentes façons avec notre équation (8.5.3). Cette "puissance" n'est pas une puissance "réelle" dans le sens que l'inductance ne fait pas perdre, sur une période, de l'énergie au circuit. La puissance réactive est dite absorbée tout simplement parce que l'inductance reçoit de l'énergie durant le premier quart de cycle du courant sinusoïdal, lorsqu'elle réagit alors en emmagasinant de l'énergie dans son champ magnétique. Alors que la puissance consommée sur une période par une résistance, "réelle", s'exprime en watts, la puissance réactive, elle, s'exprime en volt-ampère-réactifs notés VAR, afin de bien la différencier de l'autre.

Le courant efficace qui circule dans une inductance de 20 Ω placée sous une tension de 120 V est de 6 A par l'équation (8.5.3). La puissance réelle qu'elle consomme est de 0 W; la puissance réactive qu'elle absorbe, de 720 VAR par l'équation (8.5.5).

8.6 Effet sur un condensateur

a) diagramme de phase tension-courant

            Notre équation (7.9.1), avons-nous vu, nous permet de trouver la grandeur de la tension V_C (t)

aux bornes d'un condensateur. Or le courant est la dérivée de la charge, trouvée sur les armatures du condensateur, dans le temps. Il s'ensuit que la charge est, elle, l'intégrale

du courant qui y vient dans le temps. La tension aux bornes de la capacité est donc, selon nos équations (8.6.1), (8.6.2) et (8.3.1),

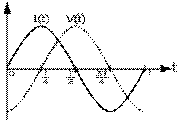
proportionnelle au négatif du cosinus du même argument que le courant. Mais encore faut-il vérifier si les polarités trouvées aux bornes du condensateur correspondent aux signes de notre dernière équation.

            Supposons que le sens positif du courant soit vers la droite. Puisque le courant est positif durant les deux premiers quarts de cycle, il s'ensuit qu'il circule alors vers la droite dans les fils reliés aux armatures: des charges positives s'accumulent donc durant tout ce temps sur l'armature de gauche, et des charges négatives, sur l'armature de droite.

                 t = T/2

            C'est à mi-période que cette accumulation est maximale puisque le courant change alors de sens. Et à ce moment, la tension est positive puisqu'elle va du positif au négatif dans le sens positif du courant.

                  t = T

            Puisque le courant est négatif durant les deux autres quarts de cycle, il s'ensuit qu'il circule vers la gauche dans les fils reliés aux armatures: des charges négatives s'accumulent donc durant tout ce temps sur l'armature de gauche, et des charges positives, sur l'armature de droite. Et c'est à la fin de la période que cette accumulation est maximale puisque le courant change alors de sens. Et, à ce moment, la tension est négative puisqu'elle va du négatif au positif dans le sens positif du courant.

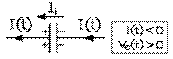         troisième quart

            La tension est donc positive et négative exactement comme l'affirme notre équation (8.6.3). Mais examinons plus en détail le cas du troisième quart de cycle: les polarités sont encore les mêmes que celles de la fin du second, soit positive sur l'armature de gauche, et négative sur l'armature de droite; et le courant dans les fils reliés aux armatures, maintenant vers la gauche: le courant de déplacement du diélectrique va du négatif au positif: le condensateur agit comme une force électromotrice alors qu'il se décharge.

            Par contre, les polarités sont négative sur l'armature de gauche et positive sur l'armature de droite durant le dernier quart de cycle alors que le courant est vers la gauche: le courant de déplacement va du positif au négatif: le condensateur agit comme une force contre-électromotrice durant sa charge.

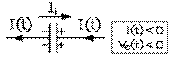        quatrième quart

            Tout comme l'inductance, donc, le condensateur agit, tantôt comme force contre-électromotrice, lorsqu'il reçoit de l'énergie qu'il emmagasine dans son champ électrique, tantôt comme force électromotrice, lorsqu'il remet l'énergie qu'il avait emmagasinée dans son champ électrique.

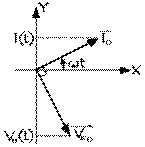
            Le terme devant la fonction négatif du cosinus de l'équation (8.6.3) est l'amplitude (ou valeur de crête) de la tension aux bornes du condensateur. La valeur de la fonction négatif du cosinus, pour un argument donné, est égale à celle de la fonction sinus si son argument est celui de la fonction cosinus, réduit de ( π / 2 ) . En quel cas la tension est dite être en retard sur le courant de ( π / 2 ) , comme le montre bien notre diagramme de Fresnel de ces vecteurs tournants.

b) réactance capacitive

Une fois notre équation (8.6.3) ainsi modifiée,

il est clair que la valeur de crête de la tension aux bornes du condensateur est proportionnelle à celle du courant qui y vient. Ces deux termes, une fois divisés par le radical de deux, deviennent la tension efficace aux bornes du condensateur et le courant efficace qui y vient. Le rapport entre, ou les valeurs de crête ou les valeurs efficaces, de la tension aux bornes sur le courant est la réactance de la capacité X_C

donnée, selon notre équation (8.6.4), par l'inverse du produit de la fréquence angulaire par la capacité elle-même. Le rapport tension sur courant ne porte pas le nom de résistance, puisque ces deux quantités ne sont pas en phase dans le cas de la capacité, mais bien déphasées de ( π / 2 ) : la capacité agit, tantôt comme une force contre-électromotrice, tantôt comme une force électromotrice. Et c'est lorsque le courant instantané est nul que la tension instantanée est maximale, et quand le courant instantané est maximal que la tension instantanée est nulle. C'est au changement de courant instantané que réagit la tension instantanée. D'où le terme réactance, plutôt que résistance.

            Le courant, requis pour obtenir une tension donnée aux bornes d'un condensateur, est d'autant plus faible que sa période est longue, puisqu'il a alors plus de temps pour amener ces charges; sa réactance est donc d'autant plus grande que la période est longue. Au cas extrême où la période est infinie -c'est le cas du courant continu- la réactance l'est également, puisque tout courant non nul, fourni pendant ce temps infini, causerait une tension infinie aux bornes du condensateur. Par contre, plus la fréquence angulaire est grande, moins le temps d'accumulation est grand, moins la charge accumulée est grande ainsi que la tension aux bornes. C'est pourquoi le rapport tension sur courant tend vers zéro lorsque la fréquence angulaire tend vers l'infini.

c) puissance réactive fournie

            Le condensateur, avons-nous vu, absorbe, comme force contre-électromotrice, de l'énergie sous forme électrique, énergie qu'elle remet ensuite comme force électromotrice. La puissance qu'elle reçoit est donnée par la loi de Joule, notre équation (5.6.6)

écrite à l'aide des équations (8.6.3), (8.6.4) et (8.3.1).

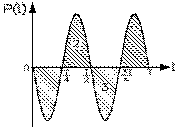
            La puissance moyenne P_m nette, reçue par le condensateur durant une période, est l'énergie nette reçue dans ce temps, divisée par cet intervalle. Or le calcul de cette énergie revient à trouver la surface sous la courbe en question, dont le croquis est donné ci-contre. La surface 2 correspondant à l'énergie reçue, emmagasinée dans le champ électrique, est égale à la surface 3 correspondant à une énergie remise: l'énergie nette reçue sur une période est nulle, et la puissance moyenne, également.

            Le produit de la tension efficace aux bornes du condensateur par le courant efficace qui y arrive n'est pas nul; mais ce n'est pas la puissance moyenne dissipée par le condensateur, vu que celui-ci ne consomme pas de puissance moyenne. Ce produit est la puissance réactive fournie Π_f

par la capacité qui peut s'écrire de différentes façons avec notre équation (8.6.5). Cette "puissance" n'est pas une puissance "réelle" dans le sens que le condensateur ne fait pas perdre, sur une période, de l'énergie au circuit. La puissance réactive est dite fournie parce que le condensateur remet l'énergie (qu'il avait reçue préalablement, dans le quart de cycle précédent) durant le premier quart de cycle du courant sinusoïdal, lorsqu'il réagit en se déchargeant.

Un condensateur de 60 Ω placé sous une tension de 120 V voit un courant de 2 A par l'équation (8.6.5). Il consomme une puissance réelle de 0 W et fournit une puissance réactive de 240 VAR par l'équation (8.6.7).

8.7 Impédance

a) le concept d’impédance

            Nous avons vu que la tension aux bornes de chacun des trois éléments examinés, résistance, inductance et condensateur, est proportionnelle au courant. Puisque tout réseau électrique est composé de ceux-ci, il s'ensuit que la tension à ses bornes V_Z l'est également. Ce que conclut Heaviside en 1886. Il nomme alors impédance Z

le rapport tension aux bornes sur le courant du réseau entre ces bornes. Elle s'exprime, tout comme la résistance et la réactance, en ohms. Elle est représentée symboliquement par un rectangle allongé dans le sens du courant.

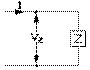
b) la puissance apparente

            La puissance consommée par une résistance, avons-nous vu, est donnée par le produit de la tension à ses bornes par le courant qui y circule: c'est une puissance réelle, qui s'exprime en watts. Le produit du courant I qui traverse une impédance Z par la tension à ses bornes V_Z ne représente pas la puissance réelle qu'elle consomme: ce produit est dit sa puissance apparente ℘

qui peut être écrite différemment à l'aide de notre équation précédente. La puissance apparente ℘ s'exprime en volt-ampères (VA).

c) le facteur de puissance

            Le facteur de puissance FP d'une impédance Z , concept introduit en 1896, est

le rapport entre la puissance P qu'elle consomme sur sa puissance apparente ℘ . Ce rapport est égal à l'unité si l'impédance est purement résistive; et égal à zéro si elle est purement réactive.

d) exemple

Une impédance de 40 Ω placée sous une tension de 120 V voit un courant de 3 A par l'équation (8.7.1). Sa puissance apparente est de 360 VA par l'équation (8.7.2). Si elle consomme une puissance réelle de 270 W, son facteur de puissance est de 0,75 par l'équation (8.7.3).

e) tensions aux bornes d’éléments en série

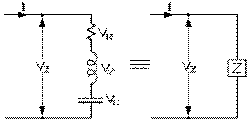
            Le même courant I circule dans une résistance, une inductance et un condensateur si ceux-ci sont placés en série. Cet ensemble peut être vu comme une impédance. La tension instantanée à ses bornes peut être calculée en termes des tensions instantanées aux bornes de chacun des trois éléments

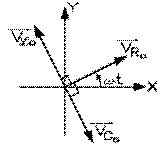
à l'aide de la deuxième loi de Kirchhoff. Ces trois tensions sont déphasées les unes par rapport aux autres, comme le montre bien le diagramme de Fresnel ci-contre de leurs vecteurs tournants.

            Notre équation (8.7.4) affirme que la tension instantanée aux bornes de l'ensemble est donnée par la somme des trois vecteurs de Fresnel.

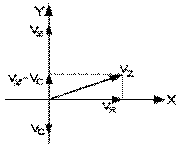
            La grandeur des vecteurs du diagramme correspond, dans chaque cas, à leur valeur de crête. Celles-ci peuvent toutes être divisées par le radical de deux: la grandeur des vecteurs correspond alors à leur tension efficace. Le diagramme alors obtenu peut être tracé au temps où l'argument ω t est nul, soit au tout début du premier quart de cycle.

            Les vecteurs de Fresnel, orientés alors selon l'axe des Y , sont de sens opposés. Leur résultante est donc leur différence. La somme vectorielle de cette dernière avec le vecteur selon l'axe X donne la grandeur de la tension efficace V_Z

par le théorème de Pythagore.

f) puissances d’éléments en série

            La multiplication de chaque vecteur tournant par le courant I donne un diagramme de Fresnel analogue, mais écrit cette fois en termes des puissances: réelle P , dans le cas du vecteur selon l'axe X (le produit V_R I ), réactive absorbée Π_b , dans le cas du vecteur selon le haut de l'axe Y (le produit V_ℒ I ), réactive fournie Π_f , dans le cas du vecteur selon le bas de l'axe Y (le produit V_C I ), et, dans le cas du vecteur résultant, apparente ℘ (le produit V_Z I ). Cette dernière est donc donnée, de façon analogue à celle de la tension aux bornes de l'impédance, par

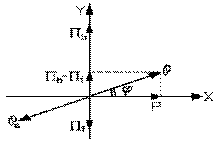
le théorème de Pythagore. La puissance apparente en question, que demande l'impédance, doit être donnée par le reste du réseau, d'ordinaire la source. Le vecteur de Fresnel de la puissance apparente donnée par la source ℘_S est de grandeur égale mais de sens opposé à celui du vecteur tournant puissance apparente ℘ de l'impédance elle-même, de telle sorte que la somme des vecteurs puissance apparente soit nulle.

            Le vecteur de Fresnel de la puissance apparente de l'impédance est en avance, de la puissance réelle qu'elle consomme, d'un angle de phase ϕ (lettre grecque phi minuscule) donnée par

son facteur de puissance FP selon notre dernière équation et son diagramme de Fresnel correspondant, ainsi que notre équation (8.7.3).

            Notre équation (8.7.6) ne s'applique pas seulement au cas où les éléments sont en série, contrairement au cas de l'équation (8.7.5). En effet, que les éléments soient en série ou en parallèle, il reste que le type de puissance, réelle, réactive absorbée ou réactive fournie, est associée à un type d'élément spécifique, vu le déphasage qui a lieu entre le courant qui y circule et la tension à ses bornes.

g) cas où les puissances réelle et apparente sont égales

            Le diagramme de Fresnel des puissances comprend un cas particulier où le réseau, qui comprend des éléments réactifs en plus de résistifs, n'apparaît, en dernière analyse, que comme une résistance.

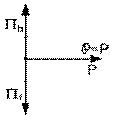
            En effet, si la puissance réactive absorbée par le réseau égale sa puissance réactive fournie

il s'ensuit de notre équation (8.7.6) que

sa puissance apparente est égale à sa puissance réelle, et, par notre équation (8.7.3), que le facteur de puissance est égal à l'unité.

8.8 Circuit inductance, résistance et condensateur en série

a) puissances et impédance

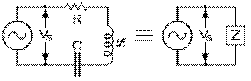
            Le courant I est le même dans chaque élément d'un circuit série comprenant une source, de tension V_S , une inductance de réactance inductive X_ℒ , une résistance R et un condensateur X_C . Notre équation (8.7.6)

devient, à l'aide des équations (8.4.6), (8.5.5), (8.6.7) et (8.7.2)

écrites en terme du courant au carré puisque c'est ce dernier qui est constant pour chaque élément. L'impédance, aux bornes de la source, soit celle des trois éléments série, est donc

une fois le courant au carré simplifié de chaque terme. Cette dernière équation devient

une fois les réactances écrites en termes de la fréquence angulaire du courant grâce aux équations (8.5.3) et (8.6.5).

b) exemple

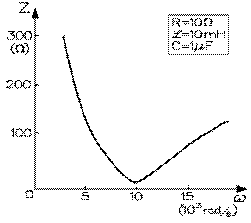
Le graphique de l'impédance d'un circuit comprenant, en série, une résistance de 10 Ω, une inductance de 10 mH et un condensateur de 1 μF de capacité, en fonction de la fréquence angulaire du courant, est donné ci-contre. Le terme inductif de notre dernière équation tend vers zéro à une fréquence angulaire très faible, alors que le terme capacité devient très grand: en fait il devient, aux faibles fréquences, le seul important et l'impédance est alors approximativement donnée par la réactance capacitive, qui varie comme l'inverse de la fréquence angulaire. Ce qui se produit sur notre graphique pour des fréquences angulaires inférieures à environ 5 000 rad/s. Le terme capacitif tend vers zéro à une fréquence angulaire très grande, alors que le terme inductif devient très grand: en fait il devient, aux grandes fréquences, le seul important et l'impédance est alors approximativement donnée par la réactance inductive, qui varie comme la fréquence angulaire. Ce qui se produit sur notre graphique pour des fréquences angulaires supérieures à environ 18 000 rad/s. L'impédance passe par une valeur minimale de 10 Ω à une fréquence angulaire de 10 000 rad/s.

c) résonance

            L'impédance d'un circuit est purement résistive lorsque sa puissance réactive absorbée est égale à sa puissance réactive fournie, avons-nous vu à notre équation (8.7.8). Cette dernière équation devient

une fois les puissances réactives écrites en terme du courant au carré à l'aide des équations (8.5.5) et (8.5.3), (8.6.7) et (8.6.5). La fréquence angulaire à laquelle l'impédance du réseau série est purement résistif est donc

la fréquence angulaire à laquelle oscille naturellement un circuit comprenant ces deux éléments réactifs, trouvée à notre équation (8.1.9): c'est pourquoi cette fréquence angulaire est dite de résonance. C'est alors, quand la source produit un courant à la fréquence à laquelle le réseau à ses bornes oscille naturellement, que son impédance est purement résistive.

            La puissance apparente, donnée par notre équation (8.7.2), est alors égale à la puissance réelle, donnée par notre équation (8.4.3), toutes deux

écrites en terme du courant au carré. Il s'ensuit que, dans le cas d'un réseau série, l'impédance à la résonance est

égale à la résistance du réseau. C'est également la valeur la plus faible de l'impédance selon notre équation (8.8.4).

d) exemple

Dans le cas du circuit déjà examiné, l'impédance purement résistive est de 10 Ω, la valeur de sa résistance. C'est également la valeur minimale que peut avoir l'impédance. La fréquence angulaire à laquelle celle-ci est obtenue est donnée par l'inverse du radical carré du produit de son inductance de 10 mH fois sa capacité de 1 μF, soit de 10 000 rad/s.

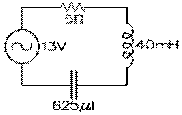
Si, aux bornes d'une source de 13 V de fréquence angulaire variable, sont placés en série une résistance de 5 Ω, une inductance de 40 mH et un condensateur de 625 μF alors que la fréquence angulaire est de 100 rad/s, les réactances des inductance et condensateur sont respectivement de 4 Ω par l'équation (8.5.3) et de 16 Ω par l'équation (8.6.5). La réactance nette du réseau est leur différence, soit 12 Ω (capacitive) et l'impédance est de 13 Ω par l'équation (8.8.3). Le courant est de 13 V divisé par 13 Ω, soit de 1 A par l'équation (8.7.1). La tension aux bornes de la résistance est alors de 5 Ω fois 1 A, soit 5 V, par l'équation (8.4.6); celle aux bornes de l'inductance, de 4 Ω fois 1 A, soit 4 V, par l'équation (8.5.3), et celle aux bornes du condensateur, de 16 Ω fois 1 A, soit 16 V, par l'équation (8.6.5). La puissance apparente, de 13 V fois 1 A, soit 13 VA, par l'équation (8.7.2); la puissance réelle, de 5 Ω fois 1 A au carré, soit 5 W, par l'équation (8.4.15); et son facteur de puissance, de 5 W divisé par 13 VA, soit 0,385, par l'équation (8.7.3). La puissance réactive absorbée par l'inductance est de 4 Ω fois 1 A au carré, soit 4 VAR, par l'équation (8.5.5); celle fournie par le condensateur, de 16 Ω fois 1 A au carré, soit 16 VAR, par l'équation (8.6.7). La source doit donc donner 5 W de puissance réelle et absorber les 12 VAR que l'impédance fournit en trop.

La fréquence angulaire de résonance de ce circuit est de 200 rad/s, par l'équation (8.8.6). Les réactances capacitive et inductives sont alors de 8 Ω chacune par nos équations (8.6.5) et (8.5.3); l'impédance, purement résistive, du circuit, de 5 Ω par l'équation (8.8.8). Le courant est de 2,6 A par l'équation (8.7.1). La tension aux bornes de la résistance est de 13 V par l'équation (8.4.6), et celles aux bornes des réactances, de 20,8 V par les équations (8.6.5) et (8.5.3).

e) réseau téléphonique

            Les premiers téléphones, avons-nous vu plus tôt dans ce chapitre, sont en circulation en 1877. Ce qui nécessite des échangeurs ainsi que des fils électriques de plus en plus nombreux au fur et à mesure que le nombre d'abonnés augmente. Au début, chaque abonné est relié à l'échangeur par un seul fil, comme dans le cas du télégraphe: la terre agit comme fil de retour. Le grand nombre d'abonnés rend énorme le nombre de fils uniques. Aussi le câble téléphonique est introduit en 1884 par la compagnie Western Electric: un faisceau de fils minces, disons 52 paires, isolés par du gutta percha ou du caoutchouc, sont recouverts par deux enveloppes de coton d'une épaisseur totale de 3 mm, puis recouverts d'une enveloppe de plomb mise à la terre. Le fil de retour remplace la mise à terre des appareils récepteur et émetteur à partir de 1892, doublant ainsi le nombre de fils requis: les 52 paires ne relient à la centrale que 52 abonnés.

            Il est réalisé assez rapidement que ce type de câble a un effet capacitif important, comme le câble sous-marin. Celui-ci peut être réduit en remplaçant le diélectrique par un de constante diélectrique plus faible. Mais l'amélioration est faible.

            Le câble apparaît donc comme un condensateur et une résistance aux ondes électriques qui s'y propagent, mimant les ondes sonores qui leur ont donné naissance: il consomme donc une puissance réelle et fournit une puissance réactive. L'impédance du circuit, qui comprend le câble, l'émetteur et le récepteur téléphoniques, est plus grande que la somme des résistances. Sir William Henry Preece (1834-1913) montre en 1887 que la distance maximale possible pour transmettre la voix de façon cohérente avec le câble téléphonique dépend et de la résistance du circuit, et de la capacité du câble. La résistance du câble est réduite à l'aide de fils conducteurs plus gros. Mais encore y a-t-il une limite à la grosseur du fil qui peut être installée. Aussi seules les villes très proches peuvent être reliées ensemble par téléphone. Heaviside reprend le travail de Preece et en 1892 montre que la solution du problème consiste à augmenter l'inductance du circuit: ou dit, autrement, installer dans le circuit des inductances qui vont absorber la puissance réactive fournie par la capacité du câble et ainsi réduire l'impédance du circuit à sa valeur la plus faible: celle correspondant à la somme de ses résistances.

            En 1899, Michael Idvorsky Pupin (1858-1935) propose, à la compagnie American Telephone et Telegraph, l'installation d'inductances à des distances fixes sur les lignes téléphoniques entre les villes afin d'obtenir la situation d'impédance minimale. La ligne de téléphone de 16 km entre New York et Newark est ainsi installée en 1902: la conversation alors entendue est aussi bonne que pour un câble sans inductance de 8 km. En 1905, celle entre New York et Philadelphie, longue de 144 km, est installée avec des bobines toroïdales placées à tous les 2 km; celle entre New York et Washington, en 1912, et entre New York et Boston, longues de 380 km en 1914. Finalement, New York et San Francisco, distantes de 5440 km, sont reliées grâce aux inductances d'une part, mais également à un nombre de répéteurs en 1915.

8.9 Circuit inductance, résistance et condensateur en parallèle

a) puissances et impédance

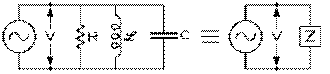
            La tension V est la même aux bornes de chaque élément d'un circuit parallèle comprenant une source, une inductance de réactance inductive X_ℒ , une résistance R et un condensateur X_C . Notre équation (8.7.6)

devient, à l'aide des équations (8.4.15), (8.5.5), (8.6.7) et (8.7.2)

écrites en terme de la tension aux bornes au carré puisque c'est cette dernière qui est constante à chaque élément. L'impédance, aux bornes de la source, soit celle des trois éléments en parallèle, est donc

une fois la tension au carré simplifiée de chaque terme. Cette dernière équation devient

une fois les réactances écrites en termes de la fréquence angulaire de la tension grâce aux équations (8.5.3) et (8.6.5).

b) exemple

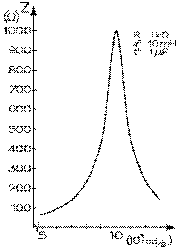
Le graphique de l'impédance d'un circuit comprenant, en parallèle, une résistance de 1000 Ω, une inductance de 10 mH et un condensateur de 1 μF de capacité en fonction de la fréquence angulaire du courant est donné à la page suivante.

c) résonance

            L'impédance d'un circuit est purement résistive lorsque sa puissance réactive absorbée est égale à sa puissance réactive fournie, avons-nous vu à notre équation (8.7.8). Celle-ci devient

une fois les puissances réactives écrites en terme de la tension au carré à l'aide des équations (8.5.5) et (8.5.3), (8.6.7) et (8.6.5). La fréquence angulaire à laquelle l'impédance du réseau série est purement résistif est donc

la fréquence angulaire à laquelle oscille naturellement un circuit comprenant ces deux éléments réactifs, donnée par notre équation (8.1.9): c'est pourquoi cette fréquence angulaire est dite de résonance. C'est quand la source produit un courant à la fréquence à laquelle le réseau à ses bornes oscille naturellement que son impédance est purement résistive.

            La puissance apparente, donnée par notre équation (8.7.2), est alors égale à la puissance réelle, donnée par notre équation (8.4.15), toutes deux

écrites en terme de la tension au carré. Il s'ensuit que, dans le cas d'un réseau parallèle, l'impédance à la résonance est

égale à la résistance du réseau. C'est également la valeur la plus grande de l'impédance selon notre équation (8.9.4).

d) exemple

Dans le cas du circuit déjà examiné, l'impédance purement résistive est de 1000 Ω, la valeur de sa résistance. C'est également la valeur maximale que peut avoir l'impédance. La fréquence angulaire à laquelle celle-ci est obtenue est donnée par l'équation (8.9.6), soit l'inverse du radical carré du produit de son inductance de 10 mH fois sa capacité de 1 μF, soit de 10 000 rad/s.

8.10 Transformation d'un réseau, de série en parallèle

a) puissances et impédance

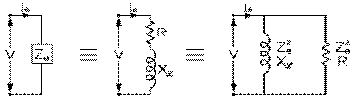
            Une bobine de fil est à la fois une résistance R , qui dissipe une puissance réelle, et une inductance ℒ , de réactance inductive X_ℒ , qui absorbe une puissance réactive. Ces deux éléments peuvent être considérés en série puisque le courant I_e que reçoit la bobine est celui que dissipe sa résistance selon l'effet Joule et qu'absorbe sa réactance inductive.

            La bobine peut donc être considérée comme un petit réseau, d'impédance Z_e , alimenté par un courant I_e lorsqu'une tension V apparaît à ses bornes. Notre équation (8.7.6), sans le terme de la puissance réactive fournie puisqu'il n'y a pas de condensateur dans ce réseau,

devient

une fois chaque terme exprimé, à l'aide des équations (8.4.15), (8.5.5) et (8.7.2), en termes du courant au carré. Notre dernière équation nous donne l'impédance de la bobine

après simplification.

            Le courant I_e qui circule dans l'impédance Z_e lorsqu'une tension V apparaît à ses bornes

est donné par notre équation (8.7.1). Il s'ensuit que notre équation (8.10.2) peut s'écrire

en termes de la tension aux bornes de l'impédance plutôt qu'en termes du courant qui y circule. Cette dernière équation est entièrement écrite en termes de la tension V aux bornes de l'impédance. Une fois simplifiée, elle exprime cette dernière

sous une forme semblable à celle de notre équation (8.9.3) avec le deuxième terme manquant. Nous avons donc une expression où les deux termes au dénominateur représentent respectivement la réactance inductive équivalente et la résistance équivalente, placées en parallèle, tel que la tension à leurs bornes est celle aux bornes de l'impédance: nous venons donc de transformer un réseau comprenant une réactance inductive et une résistance en série par un équivalent qui comprend une réactance inductive différente, et une résistance différente, en parallèle.

b) exemples

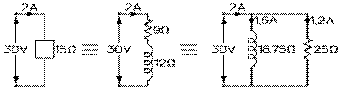
Supposons qu'un courant de 2 A circule dans une bobine sous une tension de 30 V. Son impédance, donnée par l'équation (8.7.1), est alors de 30 V divisé par 2 A, soit de 15 Ω, et sa puissance apparente, donnée par l'équation (8.7.2), de 30 V fois 2 A, soit de 60 VA. Supposons que son facteur de puissance soit de 0,6: elle consomme alors une puissance réelle de 0,6 fois 60, soit de 36 W, selon l'équation (8.7.3); et sa puissance réactive absorbée est alors de 48 VAR par l'équation (8.10.1).

La bobine peut apparaître comme une résistance et une réactance inductive, en série, dans lesquelles circule le courant de 2 A. Il s'ensuit de l'équation (8.4.15) que la résistance est de 9 Ω puisque la puissance est de 36 W et le courant, de 2 A. Il s'ensuit de l'équation (8.5.5) que la réactance inductive est de 12 Ω puisque la puissance réactive est de 48 VAR et le courant, de 2 A. (C'est tout comme s'il y avait, par l'équation (8.4.6), une tension de 18 V aux bornes de la résistance et, par l'équation (8.5.3), une de 24 V aux bornes de la réactance.)

La bobine peut également apparaître comme une résistance et une réactance inductive en parallèle, sous une tension de 30 V. Il s'ensuit de l'équation (8.4.15) que la résistance est de 25 Ω puisque la puissance est de 36 W et la tension, de 30 V. Il s'ensuit de l'équation (8.5.5) que la réactance inductive est de 18,75 Ω puisque la puissance réactive est de 48 VAR et la tension, de 30 V. (C'est tout comme si, par l'équation (8.4.6), un courant de 1,2 A circulait dans la résistance et, par l'équation (8.5.3), un de 1,6 A circulait dans la réactance.)

8.11 Alimentation du moteur électrique

a) réseau correspondant au moteur électrique

            Le moteur électrique transforme de la puissance qui provient d'un réseau électrique pour faire un travail mécanique, avons-nous vu dans notre chapitre six. Il consomme donc une puissance réelle P qu'il soutire du réseau extérieur, lorsqu'il est sous une tension V , tout comme une résistance; et ce, non seulement parce qu'il en transforme une bonne partie en puissance mécanique, mais également parce que ses résistances internes chauffent. Toute cette puissance réelle, consommée par le moteur, peut donc être symboliquement consommée par une résistance R . Mais ce moteur cause le champ magnétique dont il a besoin, avons-nous également vu. Et ce champ magnétique est ici alternatif puisque le courant qui l'alimente l'est. Il s'ensuit que le moteur agit en plus comme une réactance inductive X_ℒ qui absorbe une puissance réactive, qu'il reçoit du réseau extérieur. Il apparaît donc comme une impédance Z_e sous une tension V , et qui, donc, est alimentée par un courant I_e .

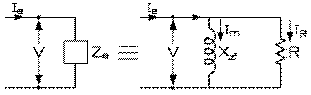
            Les résistance et réactance du moteur peuvent être représentées ou sous la forme d'un réseau interne série, ou sous la forme d'un réseau interne parallèle. Cette seconde forme est la plus utile pour ce qui va suivre. Le courant I_e requis par le moteur du réseau externe alimente, en se divisant, ces deux éléments internes, en parallèle, qui représentent le moteur. Le courant requis pour fournir le moteur en puissance réelle I_R est donc plus petit que le courant requis par le moteur en son entier I_e puisqu'une partie du courant requis va pour fournir au moteur la puissance réactive qu'il absorbe I_m .

b) condensateur parallèle

            Si un condensateur est maintenant placé en parallèle avec le moteur, celui-ci va fournir une puissance réactive, que le moteur va pouvoir absorber. Il est possible de choisir la réactance du condensateur de telle sorte que celui-ci fournisse toute la puissance réactive que le moteur absorbe. Le réseau externe, excluant le condensateur, n'a alors plus qu'à fournir la puissance réelle que le moteur consomme, et donc, un courant plus faible. Et ce, alors que le moteur fait le même travail, avec la même tension à ses bornes. Le courant d'alimentation I , qui est égal au courant I_e demandé par le moteur dans le cas où il n'y a pas de condensateur à ses bornes, diminue si une réactance capacitive est placée en parallèle avec le moteur.

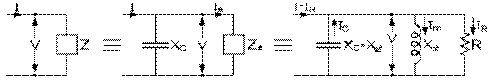
            Le réseau condensateur-moteur obtenu est alors celui examiné dans notre section 8.9, soit celui où réactances inductive, capacitive et résistance sont en parallèle. Nous avons vu que l'impédance est purement résistive lorsque la puissance réactive fournie par le condensateur est égale à la puissance réactive absorbée, et que l'impédance est alors maximale et égale à la résistance. C'est donc alors que le courant d'alimentation I , égal à I_R , est le plus faible.

c) exemple

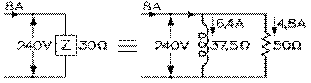
Supposons qu'un courant de 8 A circule dans un moteur placé sous une tension de 240 V. Son impédance est alors 240 V divisé par 8 A, soit de 30 Ω, selon l'équation 8.7.1), et sa puissance apparente, de 240 V fois 8 A, soit de 1920 VA, selon l'équation (8.7.2). Supposons que son facteur de puissance soit de 0,6: il consomme alors une puissance réelle de 0,6 fois 1920, soit de 1152 W selon l'équation (8.7.3); et sa puissance réactive absorbée est alors de 1536 VAR selon l'équation (8.10.1). Le moteur peut apparaître comme une résistance et une réactance inductive, en parallèle, sous une tension de 240 V. De ses puissances et de sa tension, il s'ensuit de l'équation (8.4.15) que la résistance est de 50 Ω (240 V au carré sur 1152 W) et de l'équation (8.5.5) que la réactance inductive est de 37,5 Ω (240 V au carré sur 1920 VAR). C'est tout comme si, selon l'équation (8.4.6), un courant de 4,8 A circule dans la résistance et selon l'équation (8.5.3), un de 6,4 A circule dans la réactance.

Si un condensateur, fournissant toute la puissance réactive absorbée par le moteur, est placé en parallèle avec ce dernier, il va fournir 1536 VAR sous une tension de 240 V et donc sa réactance capacitive va être de 37,5 Ω par l'équation (8.6.7); et le courant qui va circuler dans sa branche, de 240 V divisé par 37,5 Ω, soit 6,4 A, par l'équation (8.6.5). L'impédance de cet ensemble, purement résistive, est alors de 50 Ω par l'équation (8.9.8) et le courant d'alimentation, trouvé par l'équation (8.7.1), de 4,8 A, au lieu de 8 A. (Celui-ci est alors réduit par 0,6, soit le facteur de puissance du moteur.)

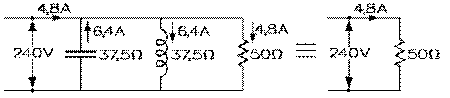
8.12 Syntonisation radio

a) ondes radio

            Le circuit oscillant avec lequel nous avons débuté notre chapitre nous a permis d'obtenir un courant alternatif sinusoïdal dont la fréquence angulaire est donnée par l'inverse du radical de son inductance fois sa capacité.

            En 1886, Heinrich Hertz (1857-1894) place deux bobines minces coaxiales l'une près de l'autre. Il relie les fils d'une des deux bobines à des aiguilles métalliques dont les extrémités se font face: ce qui constitue son circuit récepteur. Il place une bouteille de Leyde chargée aux bornes de la première bobine: ce qui constitue son circuit émetteur. Il remarque des étincelles entre ces extrémités des aiguilles, reliées à la seconde bobine, lorsqu'une bouteille de Leyde est déchargée dans la première bobine. Ce qui, soit dit en passant, ressemble fort à la première expérience de Faraday sur l'induction électromagnétique: deux bobines à proximité dans chacun des deux cas: un courant induit dans le second étant donnée la variation du courant dans le premier. La différence, à première vue, n'est que l'absence de noyau de fer pour les relier.

            Hertz embroche deux boules métalliques ajustables trouées sur ses aiguilles métalliques, constituant ainsi un condensateur ajustable, placé aux bornes de la bobine récepteur. Il remarque qu'il obtient des étincelles d'intensité maximale lorsque ce deuxième circuit est ajusté de telle sorte qu'il oscillerait naturellement à la même fréquence que le circuit émetteur. Dit autrement, à la fréquence de résonance. C'est pour cette étude approfondie des fréquences d'oscillation des circuits que l'unité de fréquence porte son nom: le hertz, noté Hz.

            Il modifie, l'année suivante, son circuit oscillant émetteur en remplaçant sa bouteille de Leyde par une bobine d'induction (comme celle de Ruhmkorff) qui, elle, fournit constamment une tension saccadée à une fréquence donnée. C'est elle qu'il relie maintenant à un éclateur muni des boules métalliques ajustables. Il obtient alors des étincelles de fréquence données avec son circuit émetteur. Il utilise, comme circuit récepteur, un anneau conducteur presque complet muni d'un éclateur minuscule et de deux petites boules métalliques ajustables, afin de pouvoir ajuster ce dernier circuit à la même fréquence d'oscillation que le premier. Il peut remarquer ensuite que ce qui cause le courant dans le second circuit est une onde électromagnétique, ce que nous n'examinerons pas ici. Mais c'est pourquoi ces ondes sont dites hertziennes.

            Guglielmo Marconi (1874-1937), reliant un côté de son circuit émetteur à la terre et l'autre à une longue tige métallique, l'antenne, réussit à transmettre sur une distance de 1 km en 1895. Après plusieurs modifications, son circuit lui permet de transmettre à travers la Manche en 1899. Et le 13 décembre 1901, Marconi réussit la première transmission transatlantique. Il est maintenant possible de relier tout récepteur, où qu'il soit ou presque, à un émetteur donné grâce aux ondes hertziennes. Les premiers navires sont munis de postes émetteurs et récepteurs en 1898, et le bureau de météorologie américain émet sur les ondes à partir de 1900 sur la côte est des Etats-Unis.

            L'élément oscillant de son circuit émetteur est encore notre circuit élémentaire du début de notre chapitre: un condensateur qui se décharge dans une inductance, et perd lentement son énergie. Mais cette énergie est perdue dans l'onde électromagnétique émise. Ce circuit ne peut donc pas émettre constamment, mais seulement par bouffées. Ce qui ne cause pas de problème pour l'émission d'ondes dont la durée requise est décidée par le code Morse: ce circuit peut émettre pendant un temps supérieur à la durée requise pour un trait en Morse.

            Reginald Aubry Fessenden (1866-1932) remplace le circuit oscillant par un alternateur qui fournit une oscillation électrique de même fréquence. L'avantage est que celui-ci la fournit constamment. Il module l'amplitude du courant, émis par son alternateur, à l'aide de son microphone, changeant ainsi la résistance de son circuit. Les ondes alors émises voient alors leur amplitude mimer le son qui a fait vibrer le microphone. Le 23 décembre 1906, il transmet la première émission radiophonique de sa station à Brent Rock, Massachusetts. Il réussit en 1907, à transmettre ainsi entre Brent Rock et l'Ecosse. Plus besoin de connaître le Morse. L'ère des télécommunications sans fil pour le grand public est maintenant établie. Il reste que le signal reçu par le récepteur ne peut pas encore être amplifié, de telle sorte que des écouteurs sont pratiquement de rigueur.

            Le nombre de stations émettrices va rapidement en augmentant. Ce qui veut dire que le circuit récepteur reçoit plus d'un signal à la fois. Il lui faut donc en choisir un et oublier les autres. Ce choix est fait en syntonisant celui désiré: en ajustant la fréquence naturelle d'oscillation du récepteur à celle de l'émetteur désiré.

b) circuit représentant l’onde radio

            Ce qui est capté par l'antenne est une onde électromagnétique qui vibre à une fréquence angulaire donnée, avec une certaine tension V_S locale. C'est elle qui est la source qui va agir sur le récepteur. La densité d'énergie dont dispose l'onde est celle qui se trouve dans ses champs électrique et magnétique locaux: c'est donc une valeur très faible. Aussi est-il raisonnable de concevoir la source comme pourvue d'une forte résistance interne R_i : puisque l'impédance du circuit comprenant le réseau de réception et la résistance interne de la source est toujours grande, le courant fourni par la source est toujours faible, ainsi que la puissance qu'elle peut transmettre au récepteur.

c) circuit récepteur des ondes

            Le récepteur comprend une bobine (une inductance ℒ et une résistance R en série) et un condensateur de capacité C en parallèle. Sa fréquence angulaire naturelle d'oscillation est donnée par l'inverse du radical carré du produit de sa capacité fois son inductance. Les inductance et résistance de la bobine peuvent être remplacées par une réactance et résistance en parallèle avec la capacité, comme nous avons-vu dans notre section 8.10.

d) impédance de la bobine du circuit récepteur

            L'impédance Z_e de la bobine est donnée par notre équation (8.10.3). Or, dans le cas des circuits de syntonisation, la valeur résistive de la bobine est toujours très faible comparée à sa réactance aux fréquences angulaires considérées. Il s'ensuit que

l'impédance de la bobine est donnée par sa réactance inductive. Notre équation (8.10.6), réécrite avec notre dernier résultat,

nous donne la valeur des réactance inductive X_ℒ et résistance R* vues en parallèle, sous tension V , et où la résistance R*

est donnée par le dernier terme sous le radical.

e) cas de la résonance du circuit récepteur

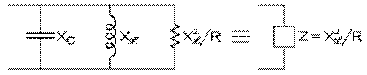
            La situation de résonance pour un réseau parallèle, avons-nous vu dans notre section 8.9, s'obtient lorsque les puissances réactives fournie et absorbée sont égales; ce qui est, puisque les tensions aux bornes des réactances inductive X_ℒ et capacitive X_C sont égales, lorsque les réactances sont égales. L'impédance Z du réseau, alors maximale et purement résistive, a la valeur de la résistance perçue en parallèle R* , soit,

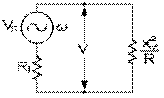
dans notre cas. La résistance totale du circuit est alors donnée par la valeur juste trouvée plus celle de la résistance interne R_i de la source. La source fournit alors le courant le plus faible qu'elle a à fournir. Mais la tension qui apparaît aux bornes du récepteur est donnée par le produit de ce courant par l'impédance encore maximale du réseau récepteur.

f) exemple

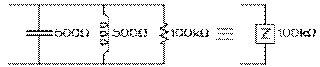
Supposons que notre onde apparaisse comme une source de 12 mV de tension, à une fréquence angulaire de 5⋅10⁵ rad/s, et de 50 kΩ de résistance interne. Supposons que la bobine du réseau récepteur soit une inductance de 1 mH de 2,5 Ω de résistance. Sa réactance inductive est alors de 500 Ω à la fréquence angulaire de la source selon notre équation (8.5.3). Et l'impédance de la bobine, donnée par notre équation (8.10.3), est bien de pratiquement 500 Ω. Sa résistance en parallèle, donnée par notre équation (8.12.3), est de 500 Ω au carré divisée par 2,5 Ω, soit de 100 kΩ. La valeur de la réactance capacitive telle que le réseau récepteur soit à la résonance est égale à celle de l'inductance, soit de 500 Ω. La capacité doit donc être de 4 nF par notre équation (8.6.5).

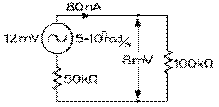
L'impédance, purement résistive, du récepteur est alors de 100 kΩ selon notre équation (8.12.4). La résistance totale du circuit, incluant la résistance interne de 50 kΩ de la source, est de 150 kΩ puisque ces deux résistances sont en série. Le courant est donc de 12 mV divisé par 150 kΩ, soit de 80 nA et la tension aux bornes du récepteur, de 100 kΩ fois 80 nA, soit de 8 mV. La puissance réelle consommée par le récepteur, donnée par l'équation (8.4.15), est de 8 mV au carré divisé par 100 kΩ, soit de 0,640 nW. La puissance réactive fournie par le condensateur à l'inductance, donnée par l'équation (8.6.7), est de 8 mV au carré divisé par 500 Ω, soit de 128 nVAR, une valeur 200 fois plus grande que la puissance réelle consommée.

g) cas de la non résonance du circuit récepteur

            Le réseau récepteur parallèle apparaît très différemment lorsque la fréquence angulaire de la source ne correspond pas à sa fréquence angulaire naturelle: en d'autres mots, lorsqu'il n'y a pas résonance. La fréquence angulaire, imposée par l'onde captée, n'est plus telle que la puissance réactive absorbée est égale à la puissance réactive fournie: en fait la différence entre ces deux valeurs excède rapidement, pour un faible changement de fréquence angulaire, la puissance réelle consommée. L'effet est que la puissance réactive (ou absorbée, ou fournie) du réseau est rapidement beaucoup plus grande que celle de la puissance consommée: elle devient le seul terme important dans l'équation de sa puissance apparente: le réseau n'apparaît alors à la source que comme une faible réactance. L'impédance totale du circuit série comprenant le réseau récepteur et la résistance interne de la source diminue donc, et le courant fourni par la source augmente, mais par une valeur limitée puisque la résistance interne est grande. La tension aux bornes du récepteur est alors plus faible puisque l'augmentation de courant ne compense pas du tout la forte diminution de son impédance. Ce poste, qui n'émet pas à la même fréquence angulaire que la fréquence angulaire naturelle du circuit récepteur, est donc capté avec une tension beaucoup plus faible. Et, puisque la puissance réelle consommée par le récepteur est donnée par la tension à ses bornes au carré, divisée par sa résistance en parallèle, celle-ci est beaucoup plus faible que dans le cas de la résonance. Le poste entendu, syntonisé, est donc celui à la fréquence de résonance. Les autres postes, émetteurs sur des fréquences différentes, sont étouffés.

h) exemple

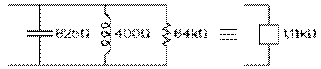
Si la fréquence angulaire de notre onde, une source de 12 mV de tension, est de 4⋅10⁵ rad/s, alors que sa résistance interne demeure de 50 kΩ, la réactance inductive de la bobine de 1 mH est alors de 400 Ω à la fréquence angulaire de la source selon l'équation (8.5.3). Et l'impédance de la bobine est bien de pratiquement 400 Ω selon l'équation (8.10.3). Sa résistance en parallèle est, elle, de 400 Ω au carré divisé par 2,5 Ω, soit de 64 kΩ par l'équation (8.12.3). La valeur de la réactance capacitive du condensateur de 4 nF est de 625 Ω par l'équation (8.6.5).

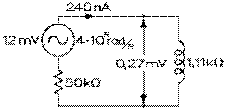
L'impédance, pratiquement celle d'une réactance inductive, du récepteur est alors de 1,11 kΩ selon notre équation (8.9.3). L'impédance totale du circuit, comprenant la résistance interne de la source de 50 kΩ et la réactance inductive de 1,11 kΩ du récepteur en série, est de pratiquement 50 kΩ selon l'équation (8.8.3) sans terme capacitif. Le courant, donné par l'équation (8.7.1), est donc de 12 mV divisé par l'impédance totale de 50 kΩ, soit de 240 nA et la tension aux bornes du récepteur, donnée par l'équation (8.5.3), de 240 nA fois 1,11 kΩ, soit de 0,266 mV. La puissance réelle consommée par le récepteur, donnée par l'équation (8.4.15), est de 0,266 mV au carré divisé par la résistance parallèle de 64 kΩ, soit de 1,11 pW, ce qui est 0,17% de celle consommée par le récepteur à la résonance. La puissance réactive nette absorbée par le récepteur, donnée par l'équation (8.5.5), de 0,266 mV au carré divisé par 1,11 kΩ, soit de 64 pVAR, a une valeur 58 fois plus grande que celle de la puissance réelle consommée.

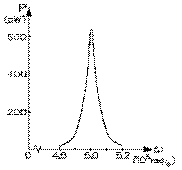
Le graphique ci-contre donne la puissance réelle captée en fonction de la fréquence angulaire émise par la source dont la force électromotrice et sa résistance interne sont de 12 mV et 50 kΩ quelle que soit sa fréquence, pour notre récepteur ajusté pour résoner à la fréquence angulaire de 5,0⋅10⁵ rad/s.

            Le récepteur syntonise des stations émettrices différentes en ajustant la valeur de sa capacité: il change alors sa fréquence angulaire naturelle et donc celle pour laquelle il entre en résonance. C'est là la raison d'être des condensateurs variables que nous avons vus dans notre chapitre sept.

i) facteur de qualité du circuit récepteur

            L'aisance qu'a un récepteur d'étouffer les postes qui émettent à des fréquences différentes de sa fréquence naturelle est son facteur de qualité. Il est défini comme le rapport de la réactance capacitive X_C du récepteur à la résonance sur la résistance série R de sa bobine. La réactance inductive est alors égale à la réactance capacitive, et la résistance parallèle de la bobine, donnée par le carré de la réactance inductive sur la résistance série. Le facteur de qualité est donc aussi égal au rapport de la résistance parallèle de la bobine sur sa réactance inductive. Et plus la résistance parallèle est grande comparée à la réactance, plus la courbe de l'impédance en fonction de la fréquence angulaire est pointue. Et puisque la tension aux bornes de la résistance en parallèle est la même que celle aux bornes des réactances, le facteur de qualité est égal au rapport des puissances réactives (fournie ou absorbée) à la résonance sur la puissance réelle consommée.

La réactance capacitive et inductive à la résonance est de 500 Ω alors que la résistance série de la bobine est de 2,5 Ω. Sa résistance parallèle est alors de 100 kΩ selon l'équation (8.12.3). La puissance réactive fournie ou absorbée alors est de 128 nVAR par les équations (8.6.7) et (8.5.5); la puissance réelle consommée, de 0,64 nW par l'équation (8.4.15). Son facteur de qualité est de 500 Ω divisé par 2,5 Ω, soit 200; ou encore, de 100 kΩ divisé par 500 Ω, soit 200 et finalement, de 128 nVAR divisé par 0,64 nW, soit 200.

8.1       Quelle est la fréquence d'oscillation trouvée lorsqu'un condensateur de 5 pF est relié à une inductance de 50 nH?

8.2       Un condensateur de 5 pF, initialement sous une tension de 50 V, est relié à une inductance de 50 nH. Quel est le courant maximal trouvé dans le circuit?

8.3       Un condensateur de 4 μF, initialement sous une tension de 20 V, est relié à une inductance de 10 nH.

       a) Quelle est la fréquence angulaire des oscillations?

       b) Quel est le courant maximal trouvé dans le circuit?

       c) Quel est l'énergie totale du circuit?

8.4       Après combien de temps l'énergie d'un condensateur de 20 μF tombe à la moitié de son énergie une fois qu'il est relié à une inductance de 50 nH?

8.5       Un condensateur de 20 pF, initialement sous une tension de 25 V, est relié à une bobine dont l'inductance est de 50 mH et la résistance, de 20 Ω.

       a) Quelle est la valeur maximale du courant?

       b) Après combien de temps la valeur de crête des oscillations ne sera que le tiers de sa valeur maximale?

8.6       Un condensateur de 20 pF, initialement sous une tension de 25 V, est relié à une bobine dont l'inductance est de 50 mH et la résistance, de 40 Ω.

       a) Après combien de temps la valeur de l'énergie du système n'est plus que 40% de sa valeur initiale?

       b) Quelle puissance moyenne le système dissipe-t-il alors?

8.7       Un condensateur de 40 pF, initialement sous une tension de 50 V, est relié à une bobine dont l'inductance est de 25 mH et la résistance, de 20 Ω. Quelle est la valeur de crête de la tension après 500 oscillations?

8.8       Un courant continu de 10 mA coule dans une bobine résistive lorsqu'elle est mise sous une tension continue de 3 V, et un courant efficace de 10 mA, lorsqu'elle est mise sous une tension efficace de 5 V de 1 kHz de fréquence.

       a) Quelle est la résistance de la bobine?

       b) Quelle est son inductance?

       c) Quelle est sa réactance?

8.9       Un circuit série comprend une source alternative de 50 V de tension oscillant à une fréquence angulaire de 5000 rad/s, une résistance de 30 Ω, une inductance de 1 mH et un condensateur de 10 μF.

       a) Quelle est la réactance du condensateur?

       b) Quelle est la réactance de l'inductance?

       c) Quelle est l'impédance du réseau aux bornes de la source?

       d) Quelle est l'amplitude du courant qui coule dans le circuit?

8.10     Un circuit série comprend une source alternative de 5 V de tension oscillant à une fréquence angulaire de 10 000 rad/s, une résistance de 40 Ω, une inductance de 7 mH et un condensateur de 1 μF.

       a) Quelle est l'impédance du circuit?

       b) Quelle est la valeur du courant qui coule dans le circuit?

       c) Quelle puissance réelle la source fournit-elle?

       d) Quelle puissance apparente la source produit-elle?

       e) Quelle puissance réactive la capacité fournit-elle?

       f) Quel est le facteur de puissance du réseau aux bornes de la source?

8.11     Un circuit série comprend une source alternative oscillant à une fréquence angulaire de 500 rad/s, une résistance de 30 Ω, une inductance et un condensateur. Une tension de 200 V apparaît aux bornes de la source, une de 120 V aux bornes de la résistance et une de 180 V aux bornes de l'inductance.

       a) Quelle est l'impédance du circuit?

       b) Quelle est la valeur de la capacité du condensateur?

       c) Quelle est la valeur de l'inductance?

       d) Quel est le facteur de puissance du réseau aux bornes de la source?

8.12     La fréquence angulaire de la source du problème précédent passe à 166,7 rad/s. La tension de la source demeure 200 V et le réseau à ses bornes est encore constitué par les mêmes éléments.

       a) Quelle est la tension aux bornes du condensateur? 

       b) Quelle est la tension aux bornes de la résistance?

       c) Quelle est la tension aux bornes de l'inductance?

       d) Quelle puissance apparente la source produit-elle?

       e) Quelle puissance réelle la source produit-elle?

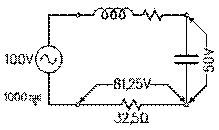
8.13     A une source de tension de 100 V sont branchés en série une bobine résistive, un condensateur et une résistance de 32,5 Ω. Lorsque la source oscille à la fréquence angulaire de 1000 rad/s, fréquence angulaire qui correspond à la fréquence d'oscillation angulaire naturelle du réseau à ses bornes, la tension est de 81,25 V aux bornes de la résistance de 32,5 Ω et de 50 V aux bornes du condensateur.

       a) Quelle est la valeur de la capacité du condensateur?

       b) Quelle est la valeur de l'inductance de la bobine résistive?

       c) Quelle est la valeur de la résistance de la bobine résistive?

8.14     La fréquence angulaire de la source du problème précédent est changée alors que la tension à ses bornes demeure 100 V et le réseau à ses bornes est encore constitué par les mêmes éléments. La tension aux bornes de la bobine est alors de 25 V et celle aux bornes de la résistance de 32,5 Ω, de 65 V.

       a) Quelle est l'impédance de la bobine résistive?

       b) Quelle puissance réelle la bobine résistive dissipe-t-elle?

       c) Quel est le facteur de puissance de la bobine résistive?

       d) Quelle est l'impédance du réseau aux bornes de la source?

       e) Quelle puissance réelle le réseau aux bornes de la source dissipe-t-il?

       f) Quel est le facteur de puissance du réseau aux bornes de la source?

       g) A quelle fréquence angulaire la source oscille-t-elle?

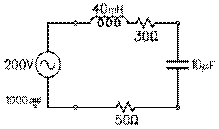
8.15     Un circuit série comprend une source alternative de 200 V de tension oscillant à une fréquence angulaire de 1 000 rad/s, une résistance de 50 Ω, une bobine résistive de 40 mH d'inductance et de 30 Ω de résistance et un condensateur de 10 μF.

       a) Quelle est la tension aux bornes du condensateur?

       b) Quelle est la tension aux bornes de la bobine résistive?

       c) Quelle est la puissance réelle produite par la source?

       d) Quelle est la fréquence angulaire de résonance du circuit?

       e) Quelle est la puissance réelle dissipée par la bobine résistive si la source est ajustée à la fréquence angulaire de résonance?

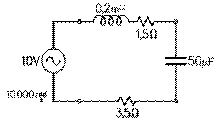
8.16     Un circuit série comprend une source alternative de 10 V de tension oscillant à une fréquence angulaire de 10 000 rad/s, une résistance de 3,5 Ω, une bobine résistive de 0,2 mH d'inductance et de 1,5 Ω de résistance et un condensateur de 50 μF.

       a) Quelle est la tension aux bornes de chaque élément du réseau aux bornes de la source?

       b) Quelle est la puissance apparente produite par la source?

       c) Quelle est la puissance réelle produite par la source?

       d) Quel est le facteur de puissance du réseau?

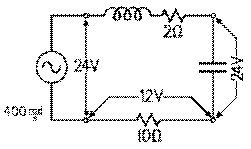
8.17     Un circuit série comprend une source alternative oscillant à une fréquence angulaire de 400 rad/s, une résistance de 10 Ω, une bobine résistive de 2 Ω de résistance et un condensateur. La tension est de 24 V aux bornes de la source, 12 V aux bornes de la résistance de 10 Ω et 24 V aux bornes du condensateur.

       a) Quelle est la valeur de la capacité du condensateur?

       b) Quelle est la valeur de l'inductance de la bobine résistive?

       c) Quelle est l'impédance du réseau aux bornes de la source?

       d) Quel est le facteur de puissance du réseau aux bornes de la source?

8.18     Un alternateur de 240 V placé aux bornes d'un moteur électrique lui fournit une puissance réelle de 2160 W lorsqu'il l'alimente avec un courant de 15 A.

       a) Quelle est l'impédance du moteur?

       b) Quel est son facteur de puissance?

8.19     Un condensateur de 37,5 Ω est placé dans le montage du problème précédent en parallèle avec le moteur.

       a) Quelle puissance réactive va-t-il fournir?

       b) Quel courant débite alors l'alternateur?

       c) Quelle réactance doit avoir le condensateur qui, remplaçant le précédent, entraîne résonance?

       d) Quelle impédance a alors l'ensemble moteur-condensateur?

8.20     Un moteur, pour fonctionner normalement, doit recevoir un courant de 25 A et être sous une tension de 240 V. Son facteur de puissance est alors de 0,6. Il est relié à une source de tension par une ligne de transmission de 4 Ω de résistance de telle sorte qu'il fonctionne normalement: qu'il reçoive 25 A sous une tension de 240 V.

       a) Quelle est l'impédance du moteur?

       b) Quelle puissance réelle consomme-t-il?

       c) Quelle puissance réactive absorbe-t-il?

       d) Quelle puissance réelle la source produit-elle alors?

       e) Quelle est alors la tension aux bornes de la source?

8.21     Un condensateur est placé en parallèle avec le moteur du problème précédent, toujours relié à la source par l'intermédiaire de la ligne de transmission, de telle sorte que le facteur de puissance de l'ensemble moteur-condensateur soit égal à l'unité.

       a) Quelle puissance réactive le condensateur doit-il fournir?

       b) Quelle doit être la réactance du condensateur?

       c) Quel courant la ligne de transmission fournit-elle?

       d) Quelle puissance réelle la source doit-elle produire?

       e) Quelle est alors la tension aux bornes de la source?

8.22     Un condensateur est placé en parallèle avec le moteur du problème précédent, toujours relié à la source par l'intermédiaire de la ligne de transmission, de telle sorte que le facteur de puissance de l'ensemble moteur-condensateur soit égal à 0,8.

       a) Quelle puissance réactive le condensateur doit-il fournir?

       b) Quelle doit être la réactance du condensateur?

       c) Quel courant la ligne de transmission fournit-elle?

       d) Quelle puissance réelle la source doit-elle produire?

       e) Quelle est alors la tension aux bornes de la source?

8.23     L'antenne reliée à un réseau de syntonisation capte une tension de 1 mV à la fréquence syntonisée lorsqu'est réglée à 2 nF la capacité du condensateur en parallèle avec une bobine résistive dont l'inductance est de 2 mH et la résistance est de 1 Ω.

       a) A quelle fréquence le réseau est-il syntonisé?

       b) Quelle est alors l'impédance du réseau de syntonisation? 

       c) Quelle puissance réelle reçoit-il?

       d) Quelle puissance réactive le condensateur fournit-il alors?

8.24     Un réseau de syntonisation comprend un condensateur variable et une bobine résistive de 2 mH d'inductance et de 5 Ω de résistance.

       a) A quelle valeur doit être ajustée la capacité de son condensateur pour syntoniser la fréquence de 60 kHz?

       b) Quelle est alors l'impédance du réseau de syntonisation?

       c) QQuelle est la réactance de son condensateur?

       d) Quelle est l'impédance du réseau tel que déjà ajusté s'il reçoit avec son antenne une fréquence de 61 kHz?

8.25     Un réseau de syntonisation comprend un condensateur variable en parallèle avec une bobine résistive dont l'inductance est de 11 mH et la résistance est de 2,2 Ω. Cet ensemble est aux bornes d'une source oscillant à une fréquence angulaire de 100 000 rad/s, dont la force électromotrice induite est de 6,1 mV et dont la résistance interne est de 60 kΩ.

       a) A quelle valeur faut-il ajuster la capacité du condensateur pour avoir syntonisation?

       b) Quelle est alors la valeur de l'impédance du réseau de syntonisation?

       c) Quelle est alors la tension aux bornes du réseau de syntonisation?

       d) Quelle est la valeur de l'impédance du réseau aux bornes de la source si la capacité du condensateur est ajustée à 10 nF?

       e) Quelle est la nouvelle tension aux bornes de la source?

8.26     Un réseau de syntonisation comprend un condensateur variable et une bobine résistive de 40 μH d'inductance et de 2 Ω de résistance. Le poste capté avec son antenne apparaît comme une source de 1,5 mV de 2,5 MΩ de résistance qui oscille à la fréquence angulaire de 1,25⋅10⁸ rad/s.

       a) A quelle valeur doit être ajustée la capacité de son condensateur pour syntoniser ce poste?

       b) Quelle puissance réelle le réseau de syntonisation reçoit-il du poste?

       c) Quelle est la nouvelle impédance du réseau de syntonisation pour ce même poste si la capacité de son condensateur est ajustée à 2 pF?

       d) Quelle puissance réelle le réseau ainsi ajusté reçoit-il alors du poste?