CHAPITRE NEUF

RÉSEAUX ÉLECTRIQUES

            Avant 1880, les génératrices, alternatives et continues, ne produisent de l'électricité que sur une petite échelle, pour quelques bâtiments rapprochés seulement. Les premières génératrices ne sont pas capables de produire une puissance suffisante pour alimenter un grand nombre d'arcs électriques et plus tard, d'ampoules incandescentes, ampoules qu'Edison produit industriellement à partir de 1880, et qui fonctionnent correctement lorsque sous une tension de 110 V.

            La première génératrice assez puissante pour alimenter un grand nombre de lampes est la génératrice Jumbo d'Edison, qui fournit une puissance électrique d'environ 88 kW sous une tension de 110 V, assez pour alimenter 1000 ampoules électriques. Il lui faut faire tourner l'induit de sa génératrice à l'aide d'une machine à vapeur assez puissante pour fournir la puissance mécanique que sa génératrice transforme, en meilleure partie, en puissance électrique. Mais encore faut-il distribuer aux lampes en question cette puissance produite par sa génératrice. Et cela n'est pas une mince affaire.

9.1 Organisation d'un réseau électrique

a) réseau simple

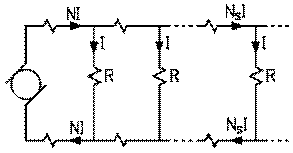
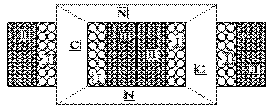
Réseau électrique simple

            Les N lampes d'un réseau électrique apparaissent chacune comme une résistance R qui demande un courant I lorsque sous une tension V égale à celle fournie par la génératrice. Elles doivent donc toutes être placées en parallèle avec elle. Le courant total demandé par les N lampes en parallèle est donc N I . Ce dernier courant, produit par la génératrice, doit être distribué aux lampes à l'aide de deux câbles électriques, dont la résistance n'est pas nulle. Les câbles de distribution dissipent une puissance qui est proportionnelle au carré du courant N_s I qui leur restent à fournir aux N_s lampes qui suivent, puisque leur courant diminue au fur et à mesure que les câbles le distribuent aux lampes. Le nombre de lampes qu'il est possible de satisfaire est donc limité, puisque la puissance dissipée par les câbles de distribution, proportionnelle au carré du nombre de lampes, va devenir, à partir d'un certain nombre, comparable à la puissance fournie à ces dernières.

b) réseau divisé en secteurs

Alimentation de secteurs par des artères

            La solution qu'utilise Edison en 1880 est de diviser en secteurs l'ensemble des lampes à alimenter. Chaque secteur est relié à la génératrice à l'aide d'un câble de distribution d'aller et un de retour. Ces secteurs sont tous en parallèle, sous même tension. Mais le nombre N de lampes alimentées par un même câble est alors d'autant plus faible que le nombre de secteurs est grand. Dans le cas d'un système à quatre secteurs, par exemple, le courant requis par un câble est toujours quatre fois plus faible que dans le cas d'un seul secteur, et la puissance perdue dans les câbles de distribution, seize fois plus faible. La génératrice est alors reliée aux lampes par huit câbles (quatre d'aller, quatre de retour). Ces câbles sont dits artères du réseau électrique.

c) alimentation à trois câbles

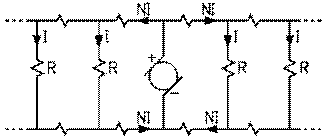
Distribution à trois câbles

            Cette solution exige la multiplication des artères avec la multiplication des lampes à alimenter. Edison (et, indépendamment, Hopkinson) invente en 1882 un système de distribution à trois câbles qui permet de doubler le nombre de lampes raccordées pour une même perte de puissance dans les câbles. Les lampes, avons-nous vu, fonctionnent correctement sous une tension de 110 V. Edison forme des doubles secteurs; il place deux génératrices, qui fournissent leur courant chacune sous une tension de 110 V, de telle sorte qu'un de leurs câbles d'alimentation de leurs secteurs soit commun.

            Chaque double secteur, comprenant maintenant deux fois plus de lampes, soit 2 N , est alimenté par trois câbles au lieu de deux, et celui du milieu est mis à terre (sous une tension nulle). Les deux premiers câbles agissent comme câbles d'aller et de retour pour environ la moitié des 2 N lampes d'un double secteur, soit N₁ ; le deuxième et le troisième câble, comme câbles d'aller et de retour pour l'autre moitié environ des 2 N lampes du double secteur, soit N₂ . Le courant qui circule dans le premier câble est N₁ I et celui dans le troisième, N₂ I ; celui dans le deuxième câble, le fil à la terre, est leur différence (N₁ - N₂ ) I puisque les courants y circulent dans des sens opposés. Le courant du fil à la terre est donc faible, sinon nul, et la puissance qu'il consomme, de même. La puissance consommée dans les deux câbles extrêmes est pratiquement la même que dans le cas précédent où il n'y avait que N lampes.

            Ces solutions au problème de l'augmentation de l'achalandage du réseau supposent malgré tout que la longueur des câbles de transmission demeure faible, qu'il n'y a guère de distance entre la génératrice et les usagers. Cela va tant et aussi longtemps que l'usine de production est là où sont les clients, mais pas autrement. S'il faut de longs câbles, portant tout le courant requis sur une grande distance, la perte de puissance sur ceux-ci devient intolérable. C'est le problème qui se pose si l'usine productrice est à l'extérieur de la ville, par exemple.

            Il faut une nouvelle solution. Une solution à prime abord impossible: faire produire à la génératrice un faible courant sous une forte tension, et distribuer cette puissance, une fois transportée aux usagers, sous la forme d'un fort courant sous une faible tension. Il n'y a, à prime abord, guère d'ennuis à bâtir une génératrice qui fournit sa puissance électrique sous une tension de, disons, 2 kV. En quel cas le courant produit n'est que de 100 A si elle fournit une puissance de 200 kW. Mais quel dispositif va transformer ce faible courant sous une forte tension en un fort courant sous une faible tension?

9.2 Le transformateur sans charge

            Dans un réseau électrique de distribution d'électricité alternative, le dispositif qui réalise simplement cette transformation, d'un faible courant en un plus fort, est le transformateur dévolteur, inventé à cet effet en 1882 par Lucien Gaulard (1850-1888). Quoiqu'il peut être dit que le montage utilisé par Faraday lors de son expérience du 29 août 1831 constitue le premier transformateur, il reste que le dispositif de Gaulard a un rôle très différent.

            Nous allons examiner le fonctionnement du transformateur dans ce contexte à l'aide des théories énoncées par Hopkinson d'une part, et Heaviside et Steinmetz d'autre part, quoique ces théories n'ont été produites que par après, comme nous avons vu.

A) flux magnétique dans son cadre et courant de magnétisation

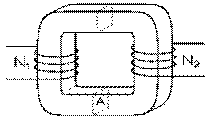
Bobinages primaire et secondaire

            D'après le travail d'Hopkinson examiné dans notre section 6.12, un flux magnétique φ_m est produit dans un circuit magnétique sous l'action d'une force magnétomotrice Γ . Le circuit magnétique est la région de l'espace où se trouve le flux magnétique. Nous avons vu dans le cas d'un cadre de section A et de périmètre L fait en fer doux de perméabilité μ , que le flux magnétique φ_m , constant dans le volume du cadre, est donné par notre équation (6.12.5)

que nous pouvons réécrire comme

si la force magnétomotrice Γ est produite par le courant de magnétisation I_M , qui alimente une bobine de N₁ spires roulées autour d'une des deux colonnes du cadre de fer doux.

            Si le courant de magnétisation alternatif I_M (t) en question varie dans le temps selon la fonction sinus avec une fréquence angulaire ω , la force magnétomotrice Γ (t) fait de même, ainsi que le flux magnétique

qui circule dans tout le cadre de fer doux. Mais encore faut-il que la perméabilité magnétique μ du noyau de fer soit une constante quel que soit le courant de magnétisation.

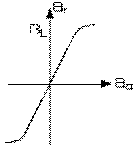
            La perméabilité magnétique est, avons-nous vu, proportionnelle à la constante magnétique K_m , selon notre équation (6.11.4), qui est le rapport des champs magnétique résultant B_r et agent B_a , selon notre équation (6.11.1). Or il existe des matériaux ferromagnétiques doux tels que la constante magnétique est, en fait, une constante pour des champs résultants B_r inférieurs à une certaine valeur limite B_L , comme le montre la courbe d'hystérésis ci-contre. Cette valeur est de l'ordre de 1,15 T. La théorie énoncée ici suppose que cette condition est satisfaite, puisqu'elle suppose que la perméabilité magnétique est constante.

b) tension induite dans chaque spire

            Le flux magnétique φ_m (t) qui traverse chaque spire de la bobine en variant dans le temps y cause une force électromotrice induite V_e (t)

selon la loi de Faraday. L'amplitude de la tension induite dans chaque spire est évidemment le terme trouvé devant la fonction cosinus, et sa valeur efficace V_e ,

cette dernière, divisée par le radical de deux.

c) tension au primaire

            La tension efficace V₁ aux bornes de la bobine de N₁ spires roulées autour d'une des colonnes du cadre de fer doux est

la somme des tensions efficaces V_e trouvées aux bornes de chacune,

parcourues par le courant de magnétisation efficace I_M . Les termes devant le courant I_M de cette dernière équation forment

la réactance inductive X_ℒ de la bobine de N₁ spires roulées autour de notre cadre de fer doux.

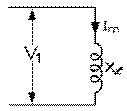
            Notre bobine agit donc comme une inductance dont la réactance inductive X_ℒ est donnée par notre équation précédente. La tension V₁ qui apparaît à ses bornes est en avance de π / 2 et sur le courant de magnétisation I_M qui y circule et sur le flux magnétique φ_m que ce courant y cause.

            Mais ce courant de magnétisation I_M va circuler dans les spires de cette bobine que si une source de tension alternative efficace V₁ est branchée à ses bornes. Le primaire requiert donc, pour créer le flux magnétique φ_m , une puissance réactive Π_b donnée par le produit de la tension à ses bornes V₁ par le courant qui y circule I_M , courant requis justement pour créer ce flux magnétique. Cette puissance réactive doit donc être fournie par la source branchée au primaire du transformateur.

d) exemple

Considérons un transformateur moderne de distribution dont la section du noyau est de 10^-2 m² , la longueur, de 2,0 m et la perméabilité, constante à 2000 fois celle du vide pour des champs magnétiques résultants inférieurs ou égaux à 1,125 T. Supposons que sa bobine de 4800 spires est alimentée par un courant sinusoïdal dont la fréquence est de 60 Hz et donc dont la fréquence angulaire est de 377 rad/s. Sa réactance inductive est alors de 109 kΩ par notre équation (9.2.8).

Si cette bobine est placée sous une tension efficace de 14,4 kV, le courant qui y circule est de 132 mA par notre équation (9.2.7). La puissance réactive absorbée est de 14,4 kV fois 0,132 A, soit 1,9 kVAR, selon notre équation (8.5.5). La tension efficace dans chaque spire est de 3,0 V par l'équation (9.2.5). L'amplitude du courant est de 132 mA fois le radical de deux, soit 184 mA, par notre équation (8.4.4). L'amplitude du flux magnétique est de 1,125⋅10^-2 T m², donnée par notre équation (9.2.3), et celle du champ magnétique, par cette dernière valeur divisée par la section du cadre, soit 1,125 T. Le transformateur opère donc dans la région où la perméabilité magnétique de son noyau est constante pour toute valeur utilisée du champ.

e) tension au secondaire

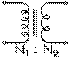
            Roulons une seconde bobine, de N₂ spires, autour de l'autre colonne du cadre de fer doux. Nous avons alors la configuration de la figure de la page 9.3. Celle-ci se représente schématiquement comme deux bobines verticales symétriques entre lesquelles se trouvent deux droites verticales représentant le noyau qui les réunit.

            La même tension efficace V_e , qui apparaît aux bornes de chaque spire de la première bobine, va apparaître aux bornes de la seconde, puisque le flux φ_m est constant dans tout le cadre. Il s'ensuit qu'une tension V₂ est induite aux bornes de cette seconde bobine, tension donnée

par la somme des tensions V_e induites dans chacune de ses N₂ spires en série.

            La tension aux bornes de la seconde bobine, dite secondaire, est reliée à celle aux bornes de la première, dite primaire. Leur rapport

est donné en divisant les équations (9.2.9) et (9.2.6) terme à terme.

f) exemple

Considérons notre transformateur dévolteur précédent dont la bobine primaire est placée sous une tension efficace de 14,4 kV et la tension efficace dans chaque spire, de 3,0 V. Une tension efficace de 240 V apparaît aux bornes de sa bobine secondaire si celle-ci comprend 80 spires selon notre équation (9.2.10).

9.3 Le transformateur en charge

a) courants dans le primaire et secondaire d’un transformateur en charge

            Plaçons maintenant comme charge une impédance Z_c aux bornes de la seconde bobine de notre transformateur. Cette impédance doit recevoir de cette seconde bobine du transformateur un courant I₂

puisque la tension V₂ du secondaire apparaît à ses bornes: le secondaire doit alors agir comme une source pour elle, lui fournissant une puissance apparente ℘ donnée par le produit de V₂ par I₂ .

            Ce courant I₂ , exigé du secondaire par l'impédance Z_c à ses bornes, cause évidemment une nouvelle force magnétomotrice Γ₂ dans le cadre de fer doux, et donc un nouveau flux magnétique φ₂ variable dans le temps.

            À cela, la bobine primaire réagit aussitôt puisque la règle de Lenz stipule qu'un circuit réagit pour s'opposer à la variation du flux magnétique qui le traverse. Le primaire exige de la source à ses bornes un courant supplémentaire I₁ pour causer une force magnétomotrice supplémentaire Γ₁

égale mais opposée à celle causée par le secondaire, afin d'annuler avec son flux magnétique variable supplémentaire φ₁ le flux magnétique variable φ₂ produit par le secondaire.

            Ce courant I₁ , exigé de la source par la bobine du primaire, peut être considéré dans une branche en parallèle avec celle du courant de magnétisation I_M . La source doit donc fournir en plus la puissance apparente ℘ requise par le primaire, donnée par le produit de la tension aux bornes du primaire V₁ par le courant supplémentaire I₁ . Or, cette puissance apparente peut être réécrite à l'aide des équations (9.3.2) et (9.2.10)

comme le produit de la tension V₂ aux bornes du secondaire fois le courant I₂ qui y circule: la puissance apparente supplémentaire fournie par la source est transformée et transférée intégralement à l'impédance Z_c aux bornes de son secondaire.

b) impédance de la charge vue au primaire

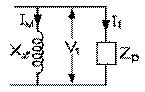
            Il nous est donc possible de visualiser le primaire du transformateur comme comprenant deux branches en parallèle: celle, purement réactive, dans laquelle circule le courant I_M qui produit le flux magnétique qui circule dans son noyau, et celle qui, puisqu'elle reçoit la puissance ℘ exigée par l'impédance Z_c, apparaît comme une impédance Z_p . Cette dernière impédance reçoit la même puissance apparente que celle aux bornes du secondaire, ce qui peut s'écrire

à l'aide de notre équation (8.7.2). L'impédance Z_p aux bornes du primaire peut alors s'écrire en termes de l'impédance de charge Z_c aux bornes du secondaire

à l'aide de notre dernière équation et de l'équation (9.3.2).

            L'impédance de charge Z_c peut être vue comme constituée d'une résistance R_c et d'une réactance, disons inductive dans ce cas, en série, dans lesquelles circule un courant I₂ . La branche supplémentaire doit donc recevoir la puissance réelle que consomme cette résistance et absorber la puissance réactive qu'absorbe cette réactance. Il s'ensuit que l'impédance vue aux bornes du primaire Z_p peut être également vue comme constituée d'une résistance R_p qui reçoit toute la puissance réelle que consomme la résistance R_c

et d'une réactance inductive qui absorbe la puissance réactive qu'absorbe la réactance

c) exemple

Considérons notre transformateur précédent dont le primaire de 4800 spires est sous une tension efficace de 14,4 kV et dont la tension efficace au secondaire de 80 spires est de 240 V. Si une impédance de 0,8 Ω est placée aux bornes de son secondaire, un courant 300 A donné par le rapport de 240 V par 0,8 Ω y circule selon l'équation (9.3.1). La puissance apparente que le transformateur doit transmettre est alors de 240 V fois 300 A, soit 72 kVA par l'équation (9.3.3). Si cette impédance peut être vue comme une résistance de 0,64 Ω en série avec une réactance inductive de 0,48 Ω, il s'ensuit de l'équation (8.4.15) que le transformateur doit fournir une puissance réelle de 0,64 Ω fois 300 A au carré, soit 57,6 KW, et il s'ensuit de l'équation (8.5.5) que le transformateur doit fournir une puissance réactive de 0,48 Ω fois 300 A au carré, soit 43,2 kVAR.

Le courant supplémentaire requis par le transformateur est de 5 A par notre équation (9.3.2). L'impédance de cette branche, de 14,4 kV divisé par 5 A, soit de 2880 Ω. Cette impédance est également donnée par le rapport des spires au carré, soit le carré de 4800 divisé par 80, fois l'impédance de 0,8 Ω, soit 2880 Ω, par notre équation (9.3.5). Cette impédance peut être perçue comme une résistance donnée par le produit du carré de 4800 divisé par 80 fois 0,64 Ω, soit 2304 Ω, par notre équation (9.3.6), et une réactance inductive en série donnée par le produit du carré de 4800 spires divisé par 80 fois 0,48 Ω, soit 1728 Ω, par notre équation (9.3.7). La puissance alors consommée est de 2304 Ω fois 5 A au carré, soit 57,6 kW, et la puissance réactive, de 1728 Ω fois 5 A au carré, soit 43,2 kVAR.

Le courant de magnétisation, celui qui circule dans la première branche du primaire, soit celle qui fournit le flux magnétique, est de 0,132 A; celui dans la branche supplémentaire, celle qui est transformée et transportée au secondaire, de 5 A, soit 38 fois plus important. Le courant de la première branche est pratiquement négligeable comparé à celui de la supplémentaire. Aussi la première branche est-elle normalement oubliée lorsque le transformateur est en charge.

Ce transformateur dévolteur permet donc de transporter une puissance apparente de 72 kVA avec un courant de 5 A seulement, au lieu d'avec un courant de 300 A. Ce qui veut dire que les pertes par effet Joule dans le câble relié à son primaire sont 3600 fois plus faibles que sans lui. L'objectif visé est bien atteint.

d) circuit correspondant au transformateur en charge

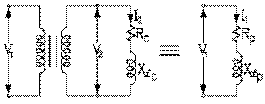
            Comme montré dans le cas spécifique précédent, la branche de magnétisation du primaire peut normalement être négligée. Il s'ensuit que l'ensemble transformateur-impédance de charge Z_c composée d'une résistance et réactance en série aux bornes de son secondaire peut être remplacé par une seule impédance Z_p , composée également d'une résistance et réactance en série, placée aux bornes où se trouve réellement son primaire. Et que cet ensemble demande un courant beaucoup plus faible que l'impédance aux bornes de son secondaire Z_c .

9.4 Transformateurs réels

a) le problème des courants de Foucault

            Remarquons bien que nous avons supposé ici que la résistance de nos deux bobines est négligeable, vu que nous n'avons pas tenu compte de la puissance qu'elles consommeraient. Nous avons également supposé que le flux magnétique produit n'existe que dans le noyau de fer. Ces deux hypothèses ne sont pas parfaitement vérifiées.

            De plus, la variation temporelle du flux magnétique dans le noyau de fer y cause des courants de Foucault, et donc la consommation d'une puissance supplémentaire, qui peut être importante et que va, encore une fois, devoir fournir la source. Le transformateur se trouve donc à consommer une certaine puissance, dont nous n'avons pas tenu compte ici. Il reste que les transformateurs modernes remettent plus de 95% de la puissance qu'ils reçoivent, et souvent, plus de 98%. Aussi allons-nous négliger cet effet dans nos équations.

            Gaulard peut sans trop de difficulté résoudre le problème de l'effet Joule dans les fils des bobines, car il lui suffit de choisir des fils dont la résistance est suffisamment faible pour que la perte de puissance dans ceux-ci soit négligeable en comparaison à la puissance transformée. Mais le problème des courants de Foucault est, lui, très sérieux. Afin de le réduire à fort peu, il forme son cadre avec une gerbe de fils de fer vernis réunis en leur extrémité un à un pour en faire un circuit magnétique complet.

            Le transformateur de Gaulard est utilisé d'abord à Londres, puis à Pittsburg par Westinghouse. Dès 1883, le noyau de fer est produit à l'aide de tôles vernies plutôt que de fils de fer minces. Il est en effet beaucoup plus facile de fabriquer et d'installer ces dernières. Après un certain temps, les bobines sont préformées de telle sorte que leurs sections sont rectangulaires. Les tôles formant le noyau sont taillées en forme de E et placées dans les sections des bobines, l'une d'un côté, l'autre de l'autre, et sont ensuite rivetées ensemble. Cette façon de faire est utilisée en 1891.

b) les deux types de transformateur

               Transformateur à colonnes

            Les bobines primaire et secondaire sont également superposées. Puisque le noyau est toujours mis à terre, la bobine qui porte le potentiel le plus faible est roulée d'abord. Un isolant est ensuite appliqué sur cette dernière, avant d'y rouler l'autre bobine.

            Dans le cas du transformateur à colonnes, les enroulements primaire et secondaire sont placés autour des deux colonnes C du noyau N de section constante, l'enroulement au plus bas potentiel I roulé en premier, et l'enroulement au plus haut potentiel II roulé ensuite sur l'autre.

       Transformateur cuirassé

            Dans le cas du transformateur cuirassé, le noyau de fer N est constitué non pas d'un seul cadre de section constante, mais de deux, collés l'un contre l'autre. Il possède donc trois colonnes C . Sa colonne centrale T a une section double du reste du cadre. C'est autour de cette dernière que les deux bobines P et S sont superposées. Il s'ensuit que les bobines sont recouvertes en majeure partie par le noyau N , d'où le terme cuirassé. Ce type de transformateur est mis au point en Amérique par William Stanley en 1886 pour Westinghouse et en Angleterre en 1887 par Ferranti. La plupart des transformateurs sont de ce type.

c) limite de la puissance apparente transformée

            Il reste qu'il y a réellement un certain échauffement du transformateur dû aux effets Joule dans le noyau et dans chacune des deux bobines. C'est pourquoi en pratique un transformateur ne peut pas transformer une puissance apparente excédent une certaine valeur limite: il chauffe alors trop, et le vernis qui recouvre les fils de ses bobinages va fondre, entraînant des courts-circuits et la destruction du transformateur.

            Ce problème de chauffage est réduit en le plaçant dans un cuve remplie d'huile, elle-même munie d'ailettes comme radiateurs.

d) transformateurs dévolteur et survolteur

            Les transformateurs, avons-nous vu, sont, au départ, utilisés pour permettre le transport d'une puissance apparente importante à l'aide d'un courant faible. Les transformateurs qui abaissent la tension sont dits dévolteurs: ils transforment la tension V₁ que reçoit leur primaire en une tension plus faible V₂ aux bornes de leur secondaire.

            Évidemment, rien n'empêche de renverser un transformateur et de l'utiliser ainsi pour hausser la tension: il est alors survolteur: la tension V₁ reçue par le primaire est alors transformée en une tension plus haute V₂ aux bornes de son secondaire. Ce rôle apparaît à partir du moment où sont construites des lignes de transmission de tension plus haute que celle des alternateurs qui la produisent. Ainsi Ferranti bâtit en 1889 des transformateurs survolteurs pour transformer la puissance active de 110 kVA reçue à 2,4 kV des alternateurs de sa station à Deptford en une à 10 kV pour son transport jusqu'à Londres.

9.5 Connexions d'un transformateur de distribution

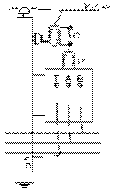
            La distribution d'électricité pour consommation domestique se fait totalement par câbles souterrains dans plusieurs pays, dont l'Angleterre, contrairement à l'Amérique du Nord, où la majeure partie se fait par câbles aériens. Les câbles souterrains prennent davantage d'importance dans certaines villes d'Amérique du Nord, comme Montréal et Québec. Ces câbles sont recouverts d'un isolant épais et placés dans une gaine métallique à la terre. Les câbles aériens qui vont aux usagers sont recouverts d'un isolant mais pas ceux, placés plus haut, qui vont aux primaires des transformateurs de distribution.

            Considérons un transformateur (dévolteur) de distribution tel celui déjà examiné dans ce chapitre, dont la tension au primaire est de 14,4 kV et celle au secondaire, de 240 V, installé au haut d'un poteau. Seule sa cuve, de forme cylindrique, est visible; le transformateur lui-même est dedans. Au sommet du cylindre se trouve une borne de porcelaine P ; et sur son côté, trois bornes A , B et T placées proches l'une de l'autre sur une droite horizontale. Le câble dont la tension est de 14,4 kV est soutenu par des isolateurs en céramique plantés au haut du poteau. Un fil qui y est connecté va à un coupe-circuit C relié à la borne de porcelaine P placée au sommet de la cuve: un conducteur se trouve enfoui au centre de la porcelaine pour permettre l'amenée de la haute tension au primaire du transformateur placé dans la cuve, qui, elle, est mise à la terre. La deuxième borne du primaire de ce transformateur est sur le côté de la cuve: c'est celle T reliée à la terre par un fil dont l'extrémité est enfouie dans le sol à l'aide d'un conducteur D qui longe le poteau.

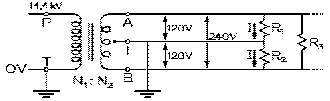
            Le secondaire de ce transformateur comprend trois bornes de sortie: une à chacune des deux extrémités de son bobinage, les bornes A et B et la troisième T , en son milieu. Puisque la tension entre les deux bornes extrêmes A et B est de 240 V, il s'ensuit que celle entre une des bornes extrêmes et celle reliée au milieu est de 120 V. La borne du milieu est reliée à la terre.

            Les trois fils isolés qui sont connectés au circuit domestique sont reliés à ces trois bornes. Un branchement d'un appareil ménager se fait entre les bornes A et T ou entre les bornes B et T . Dans un cas comme dans l'autre, l'appareil est mis sous une tension de 120 V. Aussi la moitié des prises murales sont reliées à une paire, et l'autre, à l'autre. La cuisinière électrique, la sécheuse électrique, le chauffe-eau électrique ainsi que les plinthes radiantes électriques requièrent d'être mis sous une tension de 240 V et sont donc branchés entre les bornes A et B .

            Remarquons que cet arrangement de trois fils est, dans une large mesure, l'équivalent alternatif du système de distribution à trois câbles d'Edison et Hopkinson. Si la tension à la borne A est momentanément de 100 V par rapport à la borne de terre T , il s'ensuit que celle à la borne B est alors de - 100 V par rapport à la borne T puisque la différence des tensions entre les bornes A et B est le double qu'entre A et T . Le courant circule donc de la borne A pour la moitié du circuit reliée aux bornes A et T et de la borne T pour la partie du circuit reliée aux bornes T et B . Il s'ensuit que le courant dans le fil mis à terre est la différence des courants fournis aux circuits entre A et T et entre T et B , comme dans le cas en courant continu. Ce type d'arrangement, où les tensions en A et B par rapport à T sont constamment de signes opposés, et donc déphasées de 180° ou π radians, est dit biphasé puisqu'il comporte deux tensions qui ne sont pas en phase.

9.6 Les alternateurs

            Nous avons déjà mentionné l'alternateur Siemens qui fournit du courant alternatif au théâtre Savoy de Londres en 1881 dans notre chapitre huit, ainsi que les alternateurs Siemens fournissant 250 kW sous une tension de 2 kV installés, à Londres également, en 1882, et à Pittsburg, par Westinghouse, en 1884. Il est plus que temps de voir comment ceux-ci fonctionnent.

a) pôles et segments

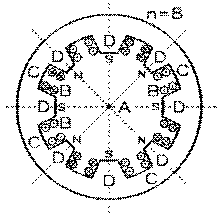
            Nous avons vu dans notre chapitre six qu'il va apparaître aux bornes d'un segment de longueur L tournant à vitesse angulaire ω sur un cercle de rayon R une force électromotrice

qui dépend du champ magnétique B là où il se trouve à ce moment.

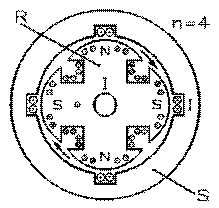
            Construisons une culasse C de fer de longueur L munie d'un nombre pair n de dents D de longueur L protubérant vers son intérieur, et roulons sur celles-ci des bobines de fil B afin de créer ainsi n pôles d'électro-aimant, alternativement nord N puis sud S . Ces électro-aimants doivent être alimentés par un courant continu pour créer leur champ magnétique.

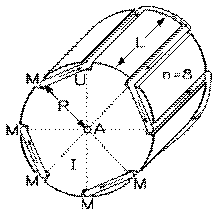
            Faisons tourner à vitesse angulaire ω , sur un arbre A dont l'axe correspond à l'axe de la culasse C , un induit I dont le noyau comprend n encoches U de longueur L dans lesquelles sont insérés à une distance R de l'arbre les segments M. Ces segments y sont roulés de telle sorte que parcourir le fil d'un bout à l'autre nous fait aller dans un sens dans une encoche U et dans le sens opposé dans la suivante.

            Le champ magnétique B va de la culasse C vers l'induit I là où se trouve un segment M qui, disons, s'enfonce dans la feuille. Il va donc de l'induit I vers la culasse C dans le segment suivant qui, lui, sort de la feuille. Le sens du courant induit est, avons-nous vu dans la section 6.5, donné par le produit vectoriel , sens qui, s'il s'enfonce dans la feuille pour le segment dans ce sens en sort pour le suivant.

            Nous avons la même tension induite, dans le même sens lors du parcours des segments, dans chacun des n segments puisqu'ils sont, au même moment, dans un même champ magnétique.

            Un segment donné est momentanément placé dans un champ magnétique qui va de la culasse C à l'induit I lorsque devant un pôle nord N , puis dans un qui va de l'induit I à la culasse C lorsque devant un pôle sud S , pour se retrouver dans la même situation qu'au début lorsqu'il se retrouve à nouveau devant un pôle nord N . Puisque la culasse comprend en tout n pôles, il s'ensuit qu'un segment rencontre n / 2 pôles nord lorsqu'il parcourt un tour complet, dans une période de rotation T_R . Durant ce temps, la tension à ses bornes a été celle correspondant à un pôle nord n / 2 fois: elle a donc vu n / 2 périodes électriques T_e durant le temps correspondant à une seule de rotation T_R . Il s'ensuit que la période électrique T_e

est plus courte que la période de rotation T_R par ce facteur n / 2 .

            La tension induite aux bornes de chaque segment en série V_S (t) , qui varie dans le temps puisque les segments voient alternativement des pôles nord et sud, est donnée

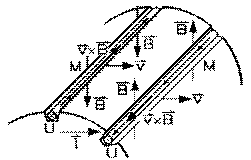
par la valeur trouvée par notre équation (9.6.1), avec la valeur instantanée B (t) du champ magnétique.

            La tension due à l'ensemble des segments, qui apparaît aux bornes de l'induit en rotation, est transférée à des points fixes à l'aide de deux balais B en contact avec deux bagues C en rotation.

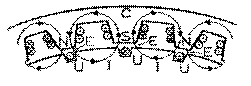
            Les lignes de champ magnétique produites par les pôles nord N des électro-aimants doivent traverser l'entrefer E , puis aller à travers le noyau de l'induit I aux pôles sud S avoisinants pour revenir à leur point de départ à travers la culasse C . Le courant continu requis pour causer le champ magnétique désiré dans l'entrefer E dépend d'abord et avant tout de l'épaisseur de ce dernier, comme nous avons déjà vu. Il doit être produit par une génératrice de courant continu auxiliaire. Les régions de l'induit, en rotation, se trouvent à couper les lignes de champ magnétique qui le parcourent, créant ainsi des courants de Foucault importants. Aussi le noyau de l'induit est-il feuilleté à partir de 1883.

            Les alternateurs, comme ceux construits par Westinghouse en 1889 qui fournissent une puissance de 125 kW sous une tension de 1 kV, débitent un courant important sous une tension assez élevée, courant qui doit circuler des bagues aux balais. Or cela peut causer problème: s'il n'y a pas un bon contact entre la bague et le balai, la différence de potentiel produit une étincelle, qui porte ce courant et qui donc chauffe ces pièces dangereusement.

b) alternateur à champ tournant

            C'est pourquoi l'alternateur à champ tournant est introduit dès 1888. Alors que, dans l'alternateur original, les segments coupent des lignes de champ magnétique fixes mais alternativement d'un sens puis de l'autre en se déplaçant à une vitesse donnée sur un cercle, dans l'alternateur à champ tournant, les segments, fixes, coupent des lignes de champ magnétique alternativement d'un sens puis de l'autre qui, elles, se déplacent à une vitesse donnée sur le cercle.

            Les bobines des électro-aimants, qui forment l'inducteur, sont placées sur un tambour en rotation, dit rotor R . Ces bobines sont alimentées en courant continu à l'aide d'un commutateur par une génératrice à courant continu, dite excitatrice. Les segments sont placés dans des encoches sur la surface interne d'une forme cylindrique creuse faite en tôles. Cet induit fixe est dit stator S . Les connexions aux deux bornes des segments connectés en série qui forment l'induit, fixes, sont directes et il n'y a donc pas de risque d'étincelles.

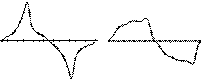
            Une tension alternative est donc induite dans les segments du stator. Mais il n'y a aucune garantie qu'elle est sinusoïdale: en fait, comme le montrent les courbes ci-contre, les premiers alternateurs ne produisent pas une telle tension. Ce qui n'est guère surprenant. Ce n'est qu'une fois qu'il est possible de produire l'équivalent d'un oscilloscope, soit vers 1897, que la forme de la tension peut être observée. Il est alors possible de modifier la forme obtenue en modifiant la forme des bobines composant les électro-aimants, et en variant quelque peu la largeur de l'entrefer en rendant les pôles saillants. La forme de la tension est maintenant vraiment celle d'une sinusoïde.

c) circuit représentant un alternateur

Alternateurs multipolaires (1901); des bobines du rotor du premier sont visibles puisque la partie supérieure de son stator est enlevée.

            Les segments dans lesquels la tension est induite sont résistifs: aussi tout alternateur a-t-il une résistance interne, comme toute pile électrique a une résistance interne. Si l'alternateur est branché sur une charge, il va débiter un courant alternatif. Ce courant alternatif cause un champ magnétique alternatif dans le noyau feuilleté du stator qui agit alors comme une inductance. Aussi le stator n'est-il pas seulement résistif, mais inductif. Et sa réactance inductive est beaucoup plus importante que sa résistance, qui peut être réduite en augmentant la section des segments de cuivre.

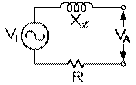
            Aussi allons-nous représenter le stator d'un alternateur à l'aide d'un cercle dans lequel se trouve le sigle sinus, pour représenter la tension efficace qui y est induite V_i , puis, à part mais à côté, le symbole de la résistance pour représenter sa résistance interne R et finalement, à part mais à côté, le symbole de la réactance inductive pour représenter sa réactance inductive interne X_ℒ . La tension efficace qui apparaît aux bornes de l'alternateur V_A n'est égale à celle induite que dans le cas où ce dernier ne débite aucun courant. C'est la tension efficace aux bornes de l'alternateur V_A que l'on cherche à maintenir constante durant son opération, ceci en ajustant la tension induite V_i .

d) tension induite aux bornes d’un alternateur

            La tension induite dans chaque segment composant le stator de l'alternateur dépend, avons-nous vu, de la valeur du champ magnétique alors subi B (t) sur toute sa longueur L lorsqu'il coupe les lignes de force magnétique à une vitesse v donnée par le produit de sa vitesse angulaire ω_R fois le rayon R . Cette tension se retrouve dans tous les segments placés dans toutes les encoches, disposées de telle sorte que la tension induite soit la même en grandeur. Ces segments sont normalement reliés de telle sorte que la tension induite dans chacun s'additionne: la tension due à l'ensemble de N segments placés dans chacune des n encoches est alors donnée par notre équation (9.6.3) modifiée

pour tenir compte, d'une part, du nombre total de segments en série et du fait que le champ magnétique apparaît osciller de façon sinusoïdale à une fréquence angulaire ω_e .

            L'amplitude de la tension induite dans le stator, le terme devant la fonction sinus dans notre équation précédente,

dépend de ses dimensions, de son nombre de pôles, du nombre de segments par encoche, de la fréquence angulaire de rotation et de l'amplitude du champ magnétique. La plupart de ces caractéristiques sont fixes une fois l'alternateur construit. Même la fréquence angulaire de rotation doit être maintenue telle que la fréquence électrique soit de 60 Hz. Il s'ensuit que la seule variable possible est l'amplitude du champ magnétique créé par les électro-aimants du rotor: c'est donc en variant celle-ci que l'amplitude de la tension induite peut varier.

            La tension induite dans le stator est donc proportionnelle au champ magnétique produit par le courant continu qui circule dans les électro-aimants du rotor, courant débité par l'excitatrice. Ce courant qui circule dans un certain nombre de spires pour former le bobinage de chaque électro-aimant est une force magnétomotrice qui cause un certain flux magnétique donné par la loi d'Hopkinson. Or le circuit magnétique comprend ici trois sections en série: un entrefer et deux tronçons dans le fer (un dans la culasse du stator, l'autre dans le noyau du rotor). La réluctance résultante est alors la somme des réluctances des trois tronçons.

            Nous avons vu que la réluctance d'une section dans le fer doux est d'autant plus faible que sa constante magnétique est grande: or celle-ci diminue fortement une fois atteint un champ magnétique de 1 T. Jusqu'à cette valeur, la réluctance des tronçons dans le fer doux est faible comparée à celle, constante, dans l'entrefer. Mais augmenter le champ une fois cette valeur atteinte augmente maintenant la réluctance totale du circuit magnétique puisque celle des tronçons de fer devient de plus en plus grande au fur et à mesure que le champ augmente. Une augmentation du courant de l'excitatrice ne cause plus une augmentation correspondante du champ magnétique, mais une plus faible. Ce qui est loin d'être une situation acceptable. Aussi le champ magnétique ne doit pas excéder 1 T dans l'entrefer.

e) exemple

Considérons un alternateur moderne qui alimente un réseau avec une tension sinusoïdale à la fréquence de 60 Hz. Son rotor comprend 36 pôles (soit 18 pôles nord et 18 pôles sud). Il tourne dont à une fréquence qui est 18 fois plus faible que la fréquence électrique, soit à une fréquence de 3,33 Hz (200 révolutions par minute) par notre équation (9.6.2). Sa vitesse angulaire est sa fréquence fois 2 π , soit 20,94 rad/s.

La culasse de fer doux feuilleté de son stator, de 2,0 m de longueur et 4,5 m de rayon interne, comprend 36 encoches (une par pôle), chacune accomodant 4 segments, pour un total de 144 segments, tous reliés en série de telle sorte que la tension induite aux bornes du stator est la somme des tensions identiques induites dans chacun. La résistance interne de ces segments et leurs raccords est de 0,2 Ω. Et leur réactance inductive interne est de 6,6 Ω.

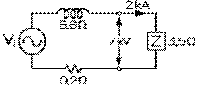
Cet alternateur est bâti pour débiter un courant de 2 kA sous une tension de 7,0 kV. Il s'ensuit que l'impédance du réseau est de 7 kV divisé par 2 kA, soit de 3,5 Ω. Cette tension est celle qui doit donc apparaître à ses bornes. Cette valeur est, comme toute tension normalement mesurée, une tension efficace. Il s'ensuit que la tension de crête demandée, soit l'amplitude, est radical de 2 fois cette valeur, soit de 9,90 kV.

Considérons d'abord le cas où l'alternateur ne fournit pas de courant. Dans un tel cas, la tension induite est égale à la tension à ses bornes et le champ magnétique du rotor doit donc fournir une tension induite de crête de 9,90 kV, soit de 365 mT selon l'équation (9.6.5).

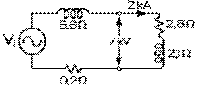
Considérons maintenant le cas où l'impédance de 3,5 Ω du réseau externe normalement à ses bornes peut être ramené à une résistance de 2,8 Ω et une réactance inductive de 2,1 Ω en série. La résistance totale du circuit est alors de 2,8 Ω plus 0,2 Ω, soit de 3,0 Ω. La réactance inductive totale, de 2,1 Ω plus 6,6 Ω, soit de 8,7 Ω.

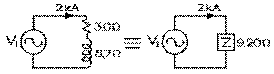
L'impédance totale du circuit est alors de 9,20 Ω par notre équation (8.8.3). La tension induite est le produit de l'impédance totale fois le courant, soit 9,20 Ω fois 2 kA, soit 18,4 kV. Sa valeur de crête, de 26,00 kV. Le champ magnétique requis est maintenant de 959 mT par l'équation (9.6.5).

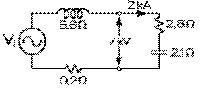
Considérons finalement le cas où l'impédance de 3,5 Ω du réseau externe normalement à ses bornes peut être ramené à une résistance de 2,8 Ω et une réactance capacitive de 2,1 Ω en série. La résistance totale du circuit est alors de 2,8 Ω plus 0,2 Ω, soit de 3,0 Ω. La réactance (inductive) totale, de 6,6 Ω moins 2,1 Ω, soit de 4,5 Ω.

L'impédance totale du circuit est alors de 5,41 Ω par notre équation (8.8.3). La tension induite est le produit de l'impédance totale fois le courant, soit 5,41 Ω fois 2 kA, soit 10,8 kV. Sa valeur de crête, de 15,30 kV. Le champ magnétique requis est maintenant de 564 mT par l'équation (9.6.5).

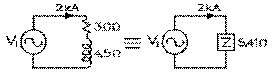
Le champ magnétique requis du rotor varie donc, dans nos exemples, de 365 mT sans charge, à 959 mT lorsque le facteur de puissance de la charge est de 0,8 dans le cas d'une charge partiellement inductive à 564 mT dans le cas d'une charge partiellement capacitive. Il se trouve donc à varier entre ces deux dernières quantités lorsque l'alternateur est en charge et que son facteur de puissance varie entre 1 et 0,8 .

Cet alternateur produit alors pour le réseau extérieur une puissance apparente nette de 7 kV fois 2 kA, soit 14 MVA par l'équation (8.7.2). La puissance réelle qu'il produit pour le réseau extérieur est, dans nos deux exemples en charge, de 2,8 Ω fois 2 kA au carré, soit de 11,2 MW, selon notre équation (8.4.15). La puissance mécanique que requiert son stator est de 3 Ω, la résistance totale du circuit, celle qui comprend sa résistance interne, fois 2 kA au carré, soit de 12 MW.

            L'excitatrice a donc comme rôle de fournir aux électro-aimants du rotor le courant continu requis pour causer un champ magnétique tel que la tension V_A trouvée aux bornes du stator de l'alternateur soit égale à sa valeur nominale, quelle que soit la charge à ses bornes, du moins dans certaines limites. Mais, du reste, d'où provient la puissance mécanique requise pour faire tourner le rotor de l'alternateur?

            Les premières génératrices, comme celles de 1881, sont entraînées par des machines à vapeur. Dans pareille machine, la vapeur, sous pression, entre dans une chambre dont une des parois, mobile, est un piston. Sa pression est telle que le piston est déplacé de telle sorte que le volume de la chambre grandit; ce qui refroidit la vapeur et diminue sa pression. Mais il reste qu'elle a entraîné un mouvement du piston, relié à une bielle qui fait, sous l'action du mouvement du piston, tourner un axe. Un mouvement de va-et-vient d'un piston est alors transformé en un mouvement rotatif. Ce qui est le cas du moteur à explosion trouvé dans les automobiles. Ce système, il va sans dire, est particulièrement inefficace.

9.7 Les alternateurs rapides

a) les turbines

            Sir Charles Algermon Parsons (1854-1931) invente la turbine à vapeur et l'utilise en tandem avec une génératrice à courant continu en 1884. La pression de la vapeur agit sur une série d'ailettes montées sur un arbre rotorique et ainsi le fait tourner aussi efficacement que possible; des ailettes fixes, placées entre celles montées sur l'arbre, sont orientées de telle sorte que la vapeur frappe ces dernières le mieux possible. Cette première turbine à vapeur, utilisée pour la génération d'électricité, tourne à 1800 révolutions par minute. L'arbre de la génératrice de tension continue est commun avec celui de la turbine. La génératrice débite alors 75 A sous une tension de 100 V, pour une puissance de 7,5 kW.

            Parsons produit en 1887 des turbo-alternateurs de 32 kVA de puissance apparente. Dans tout turbo-alternateur, les rotors des alternateur et turbine ont le même arbre de rotation.

Ceux qu'il produit en 1888 débitent 75 A sous une tension de 1 kV à la fréquence de 80 Hz alors que l'induit tourne à 4800 révolutions par minute devant deux pôles. Ceux qu'il produit 1891 débitent un courant de 50 A sous une tension de 2 kV à la fréquence de 80 Hz pour une même vitesse de rotation de l'induit.

Turbine à vapeur moderne en construction: les ailettes montées sur l'arbre rotorique sont visibles puisque la partie supérieure fixe n'est pas en place.

En 1894, afin de pouvoir augmenter davantage la puissance produite, il bâtit ses premiers turbo-alternateurs à champ tournant, à savoir dont le stator de l'alternateur comprend les segments où la tension est induite. Les rotors tournent à 3000 révolutions par minute. Le stator débite 175 A sous une tension de 2 kV à la fréquence de 50 Hz.

L'efficacité supérieure des turbo-alternateurs fait que sir Charles ne sait fournir la demande. La compagnie Westinghouse débute leur fabrication sous licence pour les Etats-Unis et la compagnie Brown-Boveri pour l'Europe continentale. La puissance apparente produite par ses turbo-alternateurs augmente encore par la suite: 1,5 MVA sous une tension de 11 kV à 1500 révolutions par minute en 1905, puis 6 MVA sous même tension et à même vitesse dès 1906. Un turbo-alternateur moderne peut produire 1 530 MVA sous une tension de 15,6 kV: le rotor de son alternateur de quatre pôles, de 7,5 m de longueur et 1,8 m de diamètre, tourne à 1500 révolutions par minute pour produire une fréquence électrique de 50 Hz.

b) transformation de puissance réelle

            Le turbo-alternateur transforme donc une puissance mécanique P_a , due à la pression de la vapeur surchauffée, en puissance électrique P_e qui, elle, est consommée par l'ensemble des résistances R_T du circuit du stator. Cette puissance mécanique développe un moment de force M_a mécanique sur l'arbre de rotation commun qui tourne avec une vitesse angulaire ω_R

donnée par notre équation (6.13.6).

            Le courant qui circule dans chaque segment placé dans un champ magnétique y cause une force magnétique qui cherche à les faire tourner. Mais ce mouvement est impossible, puisque ceux-ci sont placés dans des encoches taillées dans les tôles empilées du noyau du stator. Les segments veulent réagir pour s'opposer au changement du flux magnétique qu'ils subissent mais la force magnétique exercée sur eux est compensée par une force de réaction de la paroi de l'encoche.

            La force magnétique exercée par le champ magnétique tournant (l'agent) sur le courant du segment (patient) n'existe pas seule; la loi d'action-réaction de sir Isaac Newton exige l'existence d'une autre force, encore magnétique, égale mais de sens opposé, exercée par le courant du segment (agent) sur le pôle du champ magnétique (patient). Cette force qui agit sur les pôles du rotor cause un moment de force de réaction M_R qui cherche à le ralentir; et ce, d'autant mieux que le courant I est fort.

            Plus la quantité de vapeur fournie à la turbine est grande, plus la puissance mécanique P_a qui agit sur son rotor est grande, et donc plus il peut fournir une grande puissance électrique P_e . Mais cette dernière est fixée par les besoins des usagers composant le circuit de son stator. Si la puissance électrique P_e requise baisse soudainement, la puissance mécanique P_a fournie par la turbine est maintenant trop grande: l'équilibre est rompu et le moment de force de rappel M_R dû au courant I produit ne compense plus le moment de force mécanique M_a : l'arbre de rotation accélère. Ce qui ne peut pas être toléré: aussitôt que l'accélération est détectée, l'ouverture des vannes d'amenée de vapeur est réduite afin de réduire la puissance mécanique appliquée P_a à la valeur de la puissance électrique P_e requise. Inversement, si la puissance électrique P_e requise augmente, les rotors ralentissent puisque le moment de force de rappel M_R dû au courant I l'emporte sur le moment mécanique M_a ; et la décélération aussitôt détectée, l'ouverture des vannes d'amenée de vapeur est augmentée. La raison pour laquelle un changement de vitesse angulaire ne peut être toléré est que la fréquence électrique doit être maintenue rigoureusement à 60,0 Hz en Amérique du Nord (et 50,0 Hz en Grande-Bretagne) puisque tous les alternateurs d'un réseau sont branchés en parallèle et donc doivent avoir la même période électrique, sans quoi les tensions produites vont s'annuler.

            La vapeur utilisée par les turbo-alternateurs originaux de sir Charles Parsons est produite en brûlant du charbon; ce qui est encore le cas en Grande Bretagne et aux Etats-Unis à bien des endroits. Le mazout est également utilisé comme combustible, ainsi que l'uranium dans le cas des centrales nucléaires. La centrale d'Hydro-Québec installée à Tracy, débutée en 1964 et terminée en 1968, brûle du mazout. Elle comprend quatre groupes de turbo-alternateurs de deux pôles produisant 150 MVA chacun sous une tension de 16 kV. Les rotors tournent à 3600 révolutions par minute. La centrale d'Hydro-Québec de Gentilly 2 utilise le combustible nucléaire et produit une puissance apparente de 685 MVA.

9.8 Les alternateurs lents

a) les turbines hydrauliques

            Il existe un deuxième type de turbines, plus ancien que celui de sir Charles Parsons: la turbine hydraulique. Sous sa forme la plus simple, elle consiste en une roue à aubes, dont l'axe de rotation est horizontal, mise en rotation par le mouvement de l'eau contre ses ailerons. Son mouvement de rotation entraîne le rotor d'une génératrice. La première station hydro-électrique est mise en opération à Niagara en 1881.

La compagnie Ottawa Electric Light alimente avec un système semblable 325 lampes à arc à Ottawa en courant continu la même année. En 1889 la première centrale hydraulique produisant du courant alternatif au Canada entre en opération à Calgary, suivie de très près par une à Ottawa.

A Montréal, la première installation hydro-électrique, sur le canal Lachine, date de 1892. La compagnie Royal Electric met en chantier en 1893 une centrale hydro-électrique à Chambly, dont l'axe de rotation des alternateurs est horizontal, et qui entre en service en 1899 et produit 4,5 MW. En 1897, la Lachine Rapids Hydraulic and Land Company utilise la hauteur de chute de 3,4 m des rapides pour installer une centrale de 3 MW de puissance, ensuite augmentée à 7,6 MW. La première centrale de la Shawinigan Light and Power, mise en chantier en 1899, produit 7,5 MW en pleine opération en 1909; la seconde, en 1911, produit 29,8 MW. Cette dernière est augmentée avec l'introduction de trois nouveaux groupes, à axe horizontal comme les premiers; de plus, la hauteur de chute est passée à 43 m: la centrale produit 163 MW en 1915. Le développment des compagnies privées d'électricité continue rapidement.

Rotor T d'un alternateur hydraulique, relié par l'arbre A à sa turbine Francis, avec sa couronne C et sa conduite d'échappement P .

En 1937 le gouvernement du Québec fonde une compagnie d'état pour la production, le transport et la distribution d'électricité: Hydro-Québec, qui prend en mains quelques compagnies privées et en 1944, la centrale de Beauharnois dont la puissance produite est de 538 MW en 1948. Ce n'est qu'en 1963 que presque toutes les compagnies privées de production, transport et distribution d'électricité sont nationalisées au Québec et amalgamées à Hydro-Québec. Le second producteur d'électricité au Québec est la compagnie Alcan, qui produit avec ses propres centrales l'électricité requise pour transformer la bauxite en aluminium et pour éclairer ses usines et les petites villes où vivent ses employés.

            La turbine hydraulique a subi quelques modifications depuis ses débuts. Le modèle utilisé par Hydro-Québec est essentiellement celui produit en 1849 par James Bicheno Francis (1815-1892).

            Contrairement aux machines examinées jusqu'ici, les axes de rotation des turbines hydrauliques modernes sont verticaux comme le montre le croquis de la page précédente. La turbine est placée juste en dessous de son alternateur. Tout comme dans le couple turbo-alternateur de Parsons, les rotors de la turbine hydraulique R et de l'alternateur T comprenant les électro-aimants E ont même arbre de rotation A . Les aubes B du rotor R de la turbine sont placées selon des rayons, mais légèrement courbées. Elles reçoivent de l'eau qui provient d'une conduite forcée dont l'embouchure est au pied du barrage. Une vanne décide la quantité d'eau qui s'écoule dans la conduite forcée. L'eau de la conduite est dirigée vers une bâche en spirale qui entoure la turbine. Cette bâche, dite la couronne C , est munie d'aubes directrices fixes D incurvées vers le rotor de la turbine, pour distribuer l'eau également sur chacune des aubes du rotor. Après avoir entraîné les aubes du rotor de la turbine à sa vitesse angulaire ω_R en développant un moment de force mécanique M_a , l'eau est évacuée par une conduite d'échappement P qui comporte une cheminée de succion et un canal de fuite.

b) transfert de puissance

Couronne (à l'avant-plan) et ses aubes (à l'arrière-plan) en construction

            L'eau fait donc tourner la turbine Francis reliée à son alternateur. Dans le cas du turbo-alternateur, avons-nous vu, le débit de vapeur doit être réglé pour que la puissance mécanique fournie par la turbine égale la puissance électrique dépensée; sinon les rotors vont changer de vitesse, ce que nous avons vu être strictement inacceptable. De même ici, le débit d'eau doit être réglé pour la même raison.

            L'eau qui est amenée à la turbine voit son niveau baisser d'une hauteur de chute h qui correspond à la différence entre le niveau d'eau trouvé devant le barrage et celui trouvé à la turbine. Si l'énergie potentielle gravitationnelle dU_g d'une masse d'eau dm est considérée nulle à la hauteur de la turbine, elle est de

au niveau de l'eau devant le barrage. C'est cette énergie potentielle qui est transformée en énergie électrique lorsque la masse d'eau fait tourner la turbine s'il ne lui reste pratiquement pas d'énergie cinétique à sa sortie. Puisque cette énergie potentielle est pratiquement toute utilisée durant un laps de temps dt pour faire tourner la turbine Francis à sa vitesse angulaire d'opération, il s'ensuit que la puissance mécanique P_a est donnée par

le produit du débit d'eau fourni à la turbine dm / dt par la constante de gravitation g fois la hauteur de chute h .

c) les barrages et lacs artificiels

            Le fait que la puissance mécanique P_a fournie soit proportionnelle à la hauteur de chute h a amené la construction de barrages aussi hauts que possible: elle est de 70 m à Manic 2 (1965), 120 m à Outardes 4 (1965), 155 m à Manic 5 (1968), 94 m à Manic 3 (1976), 137 m à La Grande 2 (1980). Cela n'est pas toujours possible: la centrale de Beauharnois, sur le Saint-Laurent, qui n'a pas de lac artificiel, n'a une hauteur de chute que de 24 m et La Grande 1, une hauteur de chute de 23,5 m.

            La fréquence de rotation des rotors des turbines Francis dépend dans une large mesure de la hauteur de chute. Ils tournent à 133,33 révolutions par minute à La Grande 2, entraînant des alternateurs de 54 pôles, où la hauteur de chute est de 137 m, alors qu'ils tournent à 94,67 révolutions par minute à Beauharnois, entraînant des alternateurs de 76 pôles, où la hauteur de chute n'est que de 24 m.

            Construire un énorme barrage a l'avantage de permettre une hauteur de chute plus considérable et donc, d'obtenir plus de puissance d'un même débit d'eau. Créer un énorme lac artificiel a également l'avantage que sécheresse ou pluie abondante n'ont guère d'influence sur son niveau d'eau. Malheureusement, d'autres facteurs entrent en ligne: ces lacs artificiels deviennent de forts contaminants de la faune de la région et ainsi affectent la vie de ses habitants non seulement par leur nouvelle existence mais aussi par cette contamination. De plus, une évaporation a lieu à partir de tout plan d'eau, évaporation d'autant plus grande que le plan d'eau est vaste et que l'air est froid: c'est pourquoi l'Atlantique Nord est constamment couvert de nuages. Une quantité d'eau importante est ainsi perdue, d'autant plus grande par rapport à la masse d'eau que le lac artificiel a une profondeur moyenne faible. Ce problème est beaucoup plus important pour les barrages de la Grande Rivière, situés sur un terrain relativement peu accidenté, retenant des lacs de grande superficie mais de profondeurs moyennes faibles, que pour ceux de la Manicouagan, en terrain plus accidenté, retenant des lacs de plus faible superficie mais de plus grande profondeur moyenne.

            Évidemment, rien n'empêche de construire plusieurs barrages retenant des lacs artificiels beaucoup plus petits sur la même rivière plutôt qu'un seul: la même puissance est obtenue alors du même débit d'eau. Les pertes par évaporation sont fortement réduites, les coûts de construction des barrages, également, ainsi que la contamination produite. Le seul inconvénient est une plus grande fluctuation possible du niveau de chute, mais, après tout, Hydro-Québec s'accomode bien de centrales au fil des eaux comme celles de Carillon et de Beauharnois, où il n'y a pas du tout de lac artificiel, et donc aucune contamination à ce niveau.

            Remarquons pour terminer cette section l'avantage du barrage à fil d'eau (choisi parce qu'il n'y a pas vraiment de modification profonde de l'environnement) par rapport à une centrale thermique. Pratiquement toute l'énergie gravitationnelle de l'eau est transformée en énergie électrique dans le cas de la centrale hydro-électrique. Seulement environ 40% de l'énergie thermique est transformée en énergie électrique dans les meilleurs turbo-alternateurs. Ceci ne peut pas être amélioré pour des raisons qui dépendent du cycle de Carnot et qui dépassent les limites de ce cours. Il s'ensuit que 60% de l'énergie est perdue sous forme de chaleur. Le mazout et le charbon ne sont pas renouvelables contrairement à l'eau de la rivière, et leur combustion produit des déchets toxiques qui doivent être interceptés. De même pour l'uranium, dont les déchets doivent être traités avec soin.

            L'inconvénient sérieux des centrales hydro-électriques est que celles-ci doivent être situées là où le lit d'un cours d'eau assez important change de niveau par une valeur assez importante; ce qui est souvent fort loin des villes importantes, quand pareils cours d'eau existent; alors qu'une centrale thermique peut d'ordinaire être située près de celles-ci. Les pertes de puissance lors du transport peuvent être bien plus facilement minimisées avec un réseau de centrales thermiques qu'avec un réseau de centrales hydro-électriques comme celui d'Hydro-Québec.

9.9 Le transport de puissance

a) l’utilisation de transformateurs survolteurs

            Nous avons vu, lors de notre étude du transformateur en charge, l'avantage du transformateur dévolteur: le courant, relativement faible, qui provient de la ligne de transmission peut alors être transporté sous une tension supérieure à la tension fournie aux usagers, et être transformé en un courant beaucoup plus considérable sous une tension plus faible par le transformateur. C'est ainsi que le turbo-alternateur bâti par sir Charles Parsons en 1888 débite un courant de 75 A sous une tension de 1 kV, et que celui de 1891, débite un courant de 50 A sous une tension de 2 kV. La tension de transport est ainsi plus élevée et la perte par effet Joule dans les fils, plus faible.

            La tension, sous laquelle le courant de la ligne de transmission est transporté, peut être plus élevée que celle produite par l'alternateur si celui-ci est relié à la ligne par l'intermédiaire d'un transformateur survolteur. Nous avons déjà vu que Ferranti bâtit en 1889 des transformateurs survolteurs pour transformer la puissance reçue à 2,4 kV des alternateurs de sa station à Deptford en une à 10 kV pour son transport dans une ligne souterraine jusqu'à Londres. Ses transformateurs survolteurs peuvent alors transformer une puissance active de 110 kVA.

b) câbles souterrains

            Son câble est composé d'un fil de cuivre interne de 160 mm² de section qui est recouvert d'un papier imprégné de cire de 6 mm d'épaisseur comme isolant. L'ensemble est placé dans un tube coaxial de cuivre de même section, lui-même recouvert de 6 mm de l'isolant et ensuite inséré dans un tube de fer de 30 mm de rayon externe. Les courants vont et viennent dans les deux conducteurs de cuivre. La résistance de pareil système est donnée par la résistivité du cuivre utilisé, fois la somme de longueurs de chaque conducteur divisée par la section de chacun. Mais celui-ci agit également comme un condensateur vu que les surfaces interne du conducteur externe et externe du conducteur interne sont séparées par un diélectrique. Cette capacité apparaît aux bornes de la ligne reliées aux transformateurs.

c) câbles aériens

            Alors qu'en Grande-Bretagne les lignes de transmission de haute tension sont enfouies dans le sol, celles-ci sont aériennes en Amérique: les deux fils conducteurs de cuivre qui relient les deux bornes du transformateur survolteur au transformateur dévolteur sont fixées à l'aide d'isolateurs en porcelaine au haut des poteaux de bois à environ un mètre l'un de l'autre. La résistance de pareille ligne se trouve de la même façon que l'autre; mais sa capacité est énormément plus faible comme la distance entre celles-ci est tellement plus grande, tellement que nous pouvons la négliger ici.

            Par contre, les courants, égaux mais de sens opposés, portés par chacun des deux fils causent des champs magnétiques qui ont tendance à s'additionner dans la région qui les sépare et à s'annuler ailleurs. Pareille ligne cause donc une région de champ magnétique résultant importante, de telle sorte que la ligne agit comme une inductance non négligeable. Et alors qu'il est toujours possible de réduire la résistance de la ligne en augmentant la section des fils de cuivre, il n'est pas possible de réduire pour la peine sa réactance inductive: elle est de l'ordre de 0,5 Ω par km. Aussi une ligne aérienne apparaît essentiellement comme une résistance et une réactance inductive en série.

d) exemple

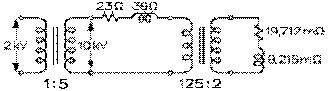
Considérons un alternateur dont la tension aux bornes du primaire de son transformateur survolteur de rapport des spires 1:5 est de 2,0 kV. La tension aux bornes du secondaire de ce dernier est de 10,0 kV. La ligne de transmission qui relie le secondaire du transformateur survolteur aux primaires des transformateurs dévolteurs (qui seront représentés ici par un seul équivalent à l'ensemble de ceux-ci en parallèle) est de 39 km. Elle est constituée par un fil à l'aller et un au retour, et donc par deux fils de cuivre de même section en série. La longueur du fil équivalent est donc de 78 km. La réactance inductive de la ligne est donc de 78 km fois 0,5 Ω par km, soit de 39 Ω. Le fil de cuivre choisi a une résistance de 0,3 Ω par km environ pour une résistance totale de 23 Ω. (La section de ce fil, dont la résistivité est d'environ 2⋅10^-8 Ωm, est d'environ 70 mm² et le diamètre, d'environ 10 mm.)

L'impédance de 21,76 mΩ représentant les abonnés, branchée aux bornes du secondaire du transformateur dévolteur de rapport de spires 125:2, est composée d'une résistance de 19,712 mΩ et d'une réactance inductive de 9,216 mΩ en série.

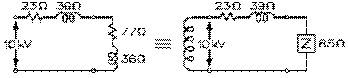
La résistance au secondaire du transformateur dévolteur peut être transportée à son primaire où elle apparaît comme une de résistance de 77 Ω par notre équation (9.3.6). De même la réactance inductive au secondaire peut être transportée au primaire où elle apparaît comme une réactance inductive de 36 Ω par notre équation (9.3.7). L'impédance aux bornes de ce secondaire elle-même en devient une au primaire de 85 Ω par notre équation (9.3.5).

Les résistances de 23 Ω de la ligne de transmission et de 77 Ω juste trouvée sont en série: la résistance totale aux bornes du secondai-re du transformateur survolteur est donc de 100 Ω. Les réactances inductive de 39 Ω de la ligne de transmission et celle de 36 Ω juste trouvée sont également en série: la réactance inductive totale aux bornes du secondaire du transformateur survolteur est donc de 75 Ω. L'impédance totale aux bornes du secondaire du transformateur survolteur est donc de 125 Ω.

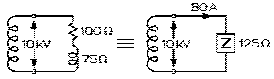
Puisque la tension aux bornes du secondaire du transformateur survolteur est de 10 kV, il s'ensuit que le courant débité par le secondaire est de 10 kV divisé par 125 Ω, soit de 80 A. La tension aux bornes du primaire du transformateur dévolteur est donnée par le produit du courant de 80 A fois l'impédance qui a été trouvée équivalente à ses bornes, soit 85 Ω: 6,8 kV.

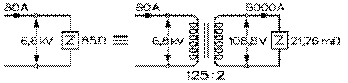
Puisque le rapport des spires du transformateur dévolteur est de 125:2, le courant dans son secondaire est 62,5 fois 80 A, soit 5000 A, et la tension aux bornes du secondaire, 6,8 kV divisé par 62,5, soit 108,8 V.

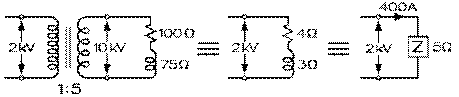
Puisque le rapport des spires du transformateur survolteur est de 1:5, le courant dans son primaire est 5 fois 80 A, soit 400 A. La résistance au secondaire du transformateur survolteur peut être transportée à son primaire où elle apparaît comme une résistance de 4 Ω par notre équation (9.3.6). De même la réactance inductive au secondaire peut être transportée au primaire où elle apparaît comme une réactance inductive de 3 Ω par notre équation (9.3.7).

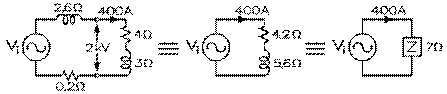
L'impédance aux bornes de ce secondaire elle-même en devient une au primaire de 5 Ω par notre équation (9.3.5). Ce qui peut également être trouvé par le fait qu'elle est donnée par le rapport de 2 kV par 400 A.

Si la résistance interne du stator de l'alternateur est de 0,2 Ω et sa réactance interne, de 2,6 Ω, il s'ensuit que la résistance totale du circuit du stator est de 4,2 Ω et sa réactance interne, de 5,6 Ω. L'impédance résultante est alors de 7,0 Ω. La tension qui doit être induite dans le stator est donc de 7,0 Ω fois 400 A, soit de 2,8 kV.

La puissance réelle donnée au consommateur est de 77 Ω fois 80 A au carré, soit de 492,8 kW; celle consommée par la ligne de transmission, de 23 Ω fois 80 A au carré, soit de 147,2 kW. Puisque la puissance réelle totale donnée au réseau est de 640,0 kW, 77% de celle-ci est disponible aux abonnés. La puissance mécanique requise de la turbine est de 4,2 Ω fois 400 A au carré, soit de 672,0 kW.

9.10 Le biphasé

a) transformateur biphasé

            L'exemple précédent montre bien que la ligne de transmission consomme une puissance qui croît avec sa longueur. Évidemment, une solution consiste à augmenter la tension sous laquelle la puissance est transportée, mais cette solution cause des problèmes pratiques que nous allons voir bientôt. Aussi une autre solution est d'abord envisagée.

            Si un montage peut être produit où le courant est nul dans le fil de retour, la résistance de la ligne de transmission ainsi que sa réactance inductive sont réduites par un facteur deux vu qu'un fil sans courant ne consomme pas et ne cause pas de champ magnétique. Nous avons déjà vu un premier montage semblable dans notre section 9.5: les bornes du secondaire du transformateur de distribution sont telles que les différences de potentiel entre celle à la terre et chacune des deux autres sont déphasées de π radians et les courants produits également, si la charge entre chacune et la terre est identique. Le courant est alors nul dans le fil de retour dit fil de terre. Pareil système est dit biphasé. Steinmetz introduit des transformateurs survolteurs avec pareils branchements à leur secondaire pour transporter la puissance produite à Niagara en 1895. Une ligne de transmission en biphasé a besoin de trois fils: deux pour porter chacun la moitié de la puissance apparente, et le troisième, pour porter un courant nul. Il va sans dire qu'il faut alors assurer que les charges aux bornes de chacun sont au moins à peu près égales pour que le courant réel dans le fil de terre soit pratiquement nul.

b) exemple

Considérons un alternateur dont la tension aux bornes du primaire de son transformateur survolteur de rapport des spires 1:10 est de 2,0 kV. La tension aux bornes du secondaire de ce dernier est de 10,0 kV des bornes extrêmes à celle du centre. Si la ligne de transmission qui relie les trois bornes du secondaire du transformateur survolteur aux primaires des transformateurs dévolteurs (qui seront représentés ici par un seul équivalent à l'ensemble de ceux-ci en parallèle) pour chaque phase est de 78 km, deux fois la longueur de l'autre. Elle est constituée par trois fils de cuivre identiques à ceux de l'exemple précédent. Le fil de retour ne porte pas de courant: c'est donc tout comme s'il n'existait pas. La réactance inductive de chaque phase de la ligne est donc de 78 km fois 0,5 Ω par km, soit de 39 Ω. Le fil de cuivre choisi a une résistance de 0,3 Ω par km environ pour une résistance totale de 23 Ω.

Le réseau de chaque phase alimenté par la ligne est celui déjà examiné dans l'exemple précédent. L'impédance totale aux bornes d'une phase du secondaire du transformateur survolteur est donc de 125 Ω, comme trouvé dans le cas précédent.

Puisque la tension aux bornes d'une phase du secondaire du transformateur survolteur est de 10 kV, il s'ensuit que le courant débité par une phase du secondaire est de 10 kV divisé par 125 Ω, soit de 80 A.

Comme dans le cas précédent, la puissance réelle donnée aux consommateurs d'une phase est de 77 Ω fois 80 A au carré, soit de 492,8 kW; celle consommée par une phase de la ligne de transmission, de 23 Ω fois 80 A au carré, soit de 147,2 kW. La puissance réelle totale donnée au réseau est le double de 640,0 kW, soit 1 280 kW. La puissance réelle donnée au consommateurs des deux phases, de 492,8 kW fois deux, soit 995,6 kW, 77% de celle donnée au réseau.

Ajouter un fil à la ligne de transmission originale en a fait une ligne biphasée. L'impédance de celle-ci est deux fois plus faible pour une même distance de ligne. Nous avons donc pu doubler la distance sans augmenter le pourcentage de pertes. Et porter avec un seul fil supplémentaire une puissance double.

9.11 Le triphasé

a) transformateur triphasé

            Oskar von Miller et Tesla réalisent tous deux une solution supérieure au biphasé en 1891. L'idée est de produire non pas deux courants de même grandeur qui vont s'annuler dans le fil de retour parce qu'ils sont déphasés de 180°, mais trois courants de même grandeur qui vont s'annuler dans le fil de retour parce qu'ils sont déphasés l'un par rapport à l'autre de 120°. Le diagramme vectoriel ci-contre montre bien que la somme des trois vecteurs de phase représentant les trois courants égaux ainsi déphasés donne bien zéro.

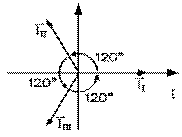
            Évidemment il faut encore le fil de terre de retour, qui normalement porte un courant négligeable et donc ne consomme pas de puissance réelle et ne produit pas de champ magnétique. Le système triphasé requiert donc quatre fils, alors que le biphasé en requiert trois. Trois de ses quatre fils portent des courants égaux, soit 75%, alors que seulement 2 des trois du biphasé portent des courants égaux, soit 67%. Ce qui est donc plus avantageux. Ajouter un seul fil à la ligne de transmission permet donc d'augmenter la puissance transportée par 50%. La première ligne européenne de triphasée, installée près de Francfort en 1891 par Miller, transmet 240 kVA sur une distance de 200 km; la première américaine, due à Tesla en 1891 également, transmet sur une distance de 175 km.

La ligne de transmission est également de 78 km comme celle du biphasé. Elle est constituée par quatre fils de cuivre de même section. Le fil de retour ne porte pas de courant: c'est donc tout comme s'il n'existait pas. La réactance inductive de chaque phase de la ligne est donc de 78 km fois 0,5 Ω par km, soit de 39 Ω. Le fil de cuivre choisi a une résistance de 0,3 Ω par km environ pour une résistance totale de 23 Ω.

Chaque phase alimente la même charge que dans le cas précédent. L'impédance totale aux bornes d'une phase du secondaire du transformateur survolteur est donc de 125 Ω.

Si la tension aux bornes d'une phase du secondaire du transformateur survolteur est de 10 kV, il s'ensuit que le courant débité par une phase du secondaire est de 10 kV divisé par 125 Ω, soit de 80 A.

Comme dans le cas précédent, la puissance réelle donnée aux consommateurs d'une phase est de 77 Ω fois 80 A au carré, soit de 492,8 kW; celle consommée par une phase de la ligne de transmission, de 23 Ω fois 80 A au carré, soit de 147,2 kW. La puissance réelle totale donnée au réseau est le triple de 640,0 kW, soit 1 920 kW. La puissance réelle donnée aux consommateurs des trois phases, de 492,8 kW fois trois, soit 1478,4 kW, 77% de celle donnée au réseau.

            Mais comment produire des tensions ainsi déphasées? Il n'est pas question ici d'utiliser un transformateur pour réaliser pareil effet. L'alternateur qui alimente un réseau triphasé a donc quelques différences par rapport à l'alternateur examiné jusqu'ici, alternateur dit monophasé. L'alternateur monophasé, avons-nous déjà vu, possède un certain nombre de segments placés dans des encoches de son stator, segments qui sont reliés en série et dont les extrémités forment les bornes du circuit interne du stator.

b) alternateur triphasé

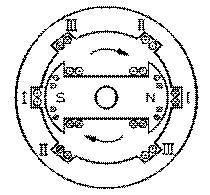
            L'alternateur triphasé diffère de l'alternateur monophasé en ce qu'il possède trois circuits internes identiques indépendants semblables à celui de l'alternateur monophasé, mais placés dans des encoches choisies pour que la tension induite dans chacun soit déphasée de 120° par rapport à la tension induite dans l'autre. Un alternateur triphasé de deux pôles pourrait alors n'avoir que deux encoches par phase, et donc six encoches en tout, disposées à 120° l'une de l'autre.

            La tension produite à une borne d'une phase oscille par rapport à celle produite à l'autre qui agit comme borne de référence. Cette dernière est alors normalement mise à la terre. Ceci se produit évidemment pour chacune des trois phases. Il s'ensuit que trois des six bornes de ce type d'alternateur sont reliées ensemble à la terre et que ce dernier n'a donc vraiment que quatre bornes, dont une de terre. Cette façon de relier les phases de l'alternateur est dite en étoile. La tension trouvée entre la borne de terre commune et une des bornes de phase est dite étoilée. C'est cette tension que l'alternateur produit aux bornes du réseau alimenté par sa phase en question.

c) tensions composée et étoilée

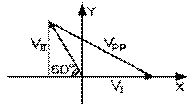
            La tension trouvée entre deux phases n'est pas égale à la tension étoilée comme le montre clairement le diagramme ci-contre. Celle-ci est dite tension composée. Nous noterons la tension composée V_pp pour la différencier de la tension étoilée, qui ne sera pas notée différemment de la tension monophasée V , vu que les tensions étoilée et monophasée sont mesurées entre la terre et la phase d'intérêt.

            Deux des trois vecteurs de tension étoilée sont indiqués sur le diagramme ci-contre. Le vecteur qui représente la tension composée V_pp est donné par l'hypoténuse

du triangle illustré de base et hauteur reliées à la tension étoilée V . La tension composée devient

une fois indiquées les valeurs des sinus et cosinus. La tension composée V_pp est donc

radical trois fois la tension étoilée V .

            La tension étoilée V est celle qui existe vraiment aux bornes de chaque phase alimentée par l'alternateur. Malheureusement en ce qui nous concerne, la tension est souvent mesurée non pas entre une phase et la terre mais bien entre deux phases, en quel cas la tension mesurée est la tension composée V_pp . Mais nous savons maintenant comment elles sont reliées.

Dans le cas de l'exemple précédent, la tension aux bornes d'une phase du secondaire du transformateur survolteur de 10 kV est une tension étoilée. La tension entre deux phases, la tension composée, est de 17,3 kV.

            La première centrale hydro-électrique au Québec à utiliser des alternateurs triphasés est celle de Rapid Plat près de Saint-Hyacinthe, qui entre en opération en 1895: ses alternateurs, construits par la Canadian General Electric, fournissent une puissance apparente de 150 kVA à une fréquence de 60 Hz.

9.12 Lignes de très hautes tensions

a) les premières lignes triphasées de l’Hydro-Québec

            En 1903, la Shawinigan Electric installe entre Shawinigan et Montréal, soit sur une distance de 135 km, une ligne triphasée de 50 kV. La tension sous laquelle la puissance est transportée augmente à 110 kV avec la ligne entre Niagara Falls et Dundas en 1910. En 1926, les lignes de transport principales en Grande Bretagne sont à 132 kV. En 1926, la Gatineau Power installe une ligne de transport entre Paugan et Toronto à 220 kV. Une ligne de transport de 120 kV est installée par la Beauharnois Light, Heat and Power entre Beauharnois et Montréal. Une ligne de ceinture de 60 kV est installée autour de Montréal. La compagnie B.C. Electric bâtit en 1957 une ligne de transmission de 360 kV et l'Ontario Hydro, une de 500 kV en 1959. La même année, Hydro-Québec construit une ligne de transport à 315 kV pour relier Bersimis 1 à son réseau. En 1965, Hydro-Québec met en service la première ligne de 735 kV, la tension la plus élevée pour une ligne de transport à ce jour. C'est avec l'examen de cette ligne que nous allons terminer ce chapitre.

b) la ligne triphasée de 735 kV

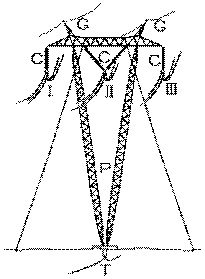
            La tension de 735 kV donnée par cette ligne, triphasée comme toutes les lignes de transport modernes, est la tension entre deux de ses phases, soit la tension composée V_pp . La tension étoilée V est donc radical trois fois moins, soit 424 kV.

c) disposition des conducteurs

            La ligne comprend trois faisceaux de quatre sous-conducteurs suspendus par des chapelets d'isolateurs C à des pylônes d'aluminium P placés à tous les 480 m. Chaque faisceau porte le courant d'une des trois phases, I , II et III , soit un courant nominal de 2 kA.

            Le fil de retour, le fil de terre T , est enfoui dans le sol et va de la base d'un pylône à l'autre. Deux fils de garde G conducteurs reliés aux pylônes sont placés au-dessus des faisceaux comme pare-foudre.

            L'illustration précédente montre ces différents fils dans le cas du pylône haubané en V, utilisé entre autres dans les lignes de transport qui relient la Baie James au reste du réseau d'Hydro-Québec. Les conducteurs des trois phases sont suspendus à ce type de pylône par des chaînes de 33 isolateurs, verticales pour les phases extérieures et en V pour la phase centrale.

d) composition des sous-conducteurs

            Les sous-conducteurs sont composés de 42 brins d'aluminium toronnés de 4,6 mm de diamètre chacun tressés sur 7 brins d'acier de 2,5 mm de diamètre: ce sont donc des fils d'aluminium munis d'une âme d'acier pour en augmenter la solidité. La résistance de chaque sous-conducteur est alors de 45 mΩ par km.

e) disposition des sous-conducteurs

            Les centres des quatre sous-conducteurs, en parallèle, sont maintenus aux arêtes d'un carré de 457 mm de côté par des supports.

            La première raison de pareille configuration en faisceaux est la suivante: le champ électrique produit par chacun des quatre sous-conducteurs au même potentiel est très fortement réduit dans la région entre ceux-ci et apparaissent alors comme un conducteur unique de 220 mm de rayon. Or nous avons vu dès notre chapitre premier le phénomène d'effluve électrique, soit la perte de charges d'un conducteur sous tension, phénomène qui devient d'autant plus important que la tension est grande. Ce qui est certes le cas ici. Mais nous avons vu également que ce phénomène est réduit d'autant plus que les rayons de courbure sont grands, d'où la nécessité de la configuration en faisceaux.

            La seconde raison est que le champ magnétique dû aux quatre sous-conducteurs, tout comme le champ électrique, est réduit dans la région entre ceux-ci. L'inductance de chaque phase de la ligne est donc réduite ainsi que sa réactance inductive.

            Les centrales du complexe de la Grande Rivière sont toutes réunies à la région de Montréal par pareilles lignes de transport triphasé à 735 kV; de même la centrale de Churchill Falls à Terre-Neuve, ainsi que plusieurs centrales du complexe de Manicouagan-Les Outardes et Bersimis. La région métropolitaine comporte également une ligne de ceinture à 735 kV.

9.1       Un transformateur dévolteur abaisse une tension de 60 Hz de 424 kV à 132,5 kV. Son cadre, de 4 m de longueur, est formé de colonnes de 0,785 m² de section. Son primaire comprend 2000 spires.

       a) Combien a-t-il de spires à son secondaire?

       b) Quel est le champ magnétique maximal dans son cadre?

9.2       Le cadre d'un transformateur dévolteur 120 V / 30 V opérant à 60 Hz a une section de 10^-4 m² , une longueur de 0,16 m et une constante magnétique de 2000. Son secondaire comprend 1250 spires.

       a) Quel est le nombre de spires de son primaire?

       b) Quelle est sa réactance inductive au primaire?

       c) Quel est son courant de magnétisation?

       d) Quel courant requiert-il si une charge de 1 kΩ purement résistive est placée aux bornes de son secondaire?

       e) Quel courant requiert-il si une charge de 100 Ω purement résistive est placée aux bornes de son secondaire?

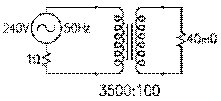
9.3       Une résistance de 40 mΩ est placée aux bornes des 100 spires du secondaire d'un transformateur. Une source de 240 V de 1 Ω de résistance interne qui oscille à 50 Hz est placée aux bornes des 3500 spires de son primaire.

       a) Quelle est la puissance dissipée par la résistance de 40 mΩ?

       b) Quelle est la fréquence de la tension à ses bornes?

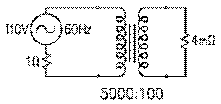
9.4       Un fer à souder dont la résistance interne est de 4 mΩ est placé aux bornes des 100 spires du secondaire d'un transformateur. Une source de 110 V de 1 Ω de résistance interne qui oscille à 60 Hz est placée aux bornes des 5000 spires de son primaire.

       a) Quel courant circule dans le fer à souder?

       b) Quelle est la fréquence de la tension à ses bornes?

9.5       Un amplificateur peut se ramener à une source et une résistance interne et un haut-parleur, à une résistance. La tension aux bornes de l'amplificateur est de 80 V quand il ne débite pas de courant; et le courant maximum qu'il débite, lorsque ses bornes sont court-circuitées par un ampèremètre, est de 5 A. Le courant débité par l'amplificateur est de 2,5 A si le haut-parleur est branché au secondaire d'un transformateur dont le primaire est connecté à l'amplificateur avec un rapport de spires primaire:secondaire de 4:2.

       a) Quelle est la résistance interne de l'amplificateur?

       b) Quelle est la résistance du haut-parleur?

       c) Quelle est la puissance consommée par le haut-parleur si le rapport de spires primaire:secondaire est de 3:2?

9.6       Le courant efficace dans chaque phase d'une ligne de transmission triphasée est de 100 A. Quel est le courant instantané dans les phases I et III si celui dans la phase II est de 50 A?

9.7       Un courant efficace de 100 A coule dans chaque phase d'une ligne de transmission triphasée dont la tension composée est de 735 kV.

       a) Quelle est la puissance apparente transportée par toute la ligne?

       b) Quel est le courant instantané dans les phases II et III si celui dans la phase I est de 141,42 A?

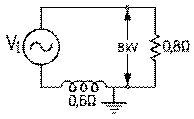                (une phase)

9.8       Un alternateur triphasé, dont la tension étoilée est de 8 kV et dont la réactance inductive est de 0,6 Ω par phase, alimente trois réseaux purement résistifs de 0,8 Ω.

       a) Quelle puissance réelle totale produit-il?

       b) Quelle est la tension induite étoilée requise dans son stator?

       c) Quelle est sa tension composée?

9.9       La puissance totale produite par les 16 groupes de turbines et alternateurs composant la centrale de LG2 à La Grande Rivière est de 5,328 GW. La hauteur de chute y est de 150 m. La fréquence de rotation des turbines Francis dont l'arbre de couche est commun au rotor des alternateurs est de 133,3 tours/minute. La tension composée produite par les alternateurs est de 13,8 kV, à une fréquence de 60,00 Hz.

       a) Quel est le nombre de pôles trouvés sur chaque stator?

       b) Quel est le débit d'eau utilisé afin de fournir toute la puissance installée?

       c) Quel est le moment de force demandé à chaque turbine?

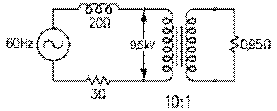
9.10     Un alternateur de 4 pôles, dont le stator, de 3 Ω résistance et de 20 Ω réactance inductive, produit une tension mono-phasée de 60 Hz de 9,5 kV aux bornes du primaire d'un transformateur dévolteur dont le rapport de spires primaire:secondaire est de 10:1. La résistance de l'usine, branchée aux bornes du secondaire, est de 0,95 Ω.

       a) Quelle est la fréquence de rotation du rotor de l'alternateur?

       b) Quelle est la résistance équivalente de l'usine vue à travers le primaire du transformateur?

       c) Quelle est la puissance réelle consommée par l'usine?

       d) Quel est le moment de force requis du moteur diésel entraînant le rotor?

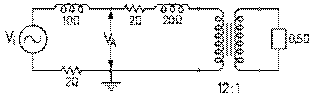                                (une phase)

9.11     Chaque phase du stator d'un alternateur triphasé, connecté en étoile, de 2 Ω de résistance et 10 Ω de réactance inductive, alimente directement une ligne de transmission de 2 Ω de résistance et de 20 Ω de réactance inductive reliée au primaire d'un transformateur dévolteur dont le rapport de spires primaire:secondaire est de 12:1. Le facteur de puissance de l'impédance de 0,5 Ω, partiellement inductive, aux bornes du secondaire est de 0,8.

       a) Quelle est l'impédance vue à travers le transformateur?

       b) Quelle est l'impédance aux bornes de l'alternateur?

       c) Quelle est l'impédance totale pour chaque phase?

9.12     Chaque phase du stator du problème précédent débite un courant de 100 A.

       a) Quelle est la tension étoilée aux bornes du secondaire de transformateur?

       b) Quelle est la tension étoilée aux bornes de l'alternateur?

       c) Quelle est la tension étoilée induite dans son stator?

       d) Quelle est la puissance réelle consommée par l'usine branchée aux trois transformateurs dévolteurs?

9.13     La tension aux bornes du stator d'un alternateur monophasé est de 14,6 kV oscillant à 60 Hz lorsque celui-ci ne débite pas de courant. Cette tension induite est maintenue

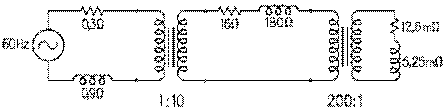
constante. La résistance interne du stator est de 0,3 Ω; sa réactance inductive interne, de 0,9 Ω. Le primaire d'un transformateur survolteur dont le rapport de spires primaire:secondaire est de 1:10 est relié au stator; son secondaire, à une ligne de transmission de 16 Ω de résistance et de 180 Ω de réactance inductive. Le primaire d'un transformateur dévolteur dont le rapport de spires primaire:secondaire est de 200: 1 est relié à la ligne; son secondaire, à une usine de 12,6 mΩ de résistance et de 5,25 mΩ de réactance inductive.

       a) Quelle est l'impédance du réseau aux bornes de l'alternateur?

       b) Quel courant débite l'alternateur?

       c) Quelle puissance apparente produit-il?

       d) 

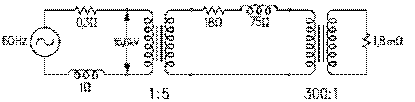
Quelle puissance réelle produit-il?

       e) Quelle puissance réelle consomme l'usine?

9.14      Le stator d'un alternateur de 54 pôles crée une tension monophasée de 15,6 kV à 60 Hz aux bornes du primaire d'un transformateur survolteur dont le rapport de spires primaire:secondaire est de 1:5. La résistance interne du stator est de 0,3 Ω; sa réactance inductive, de 1 Ω. Une ligne de transmission, de 18 Ω de résistance et de 75 Ω de réactance inductive, réunit le secondaire du transformateur survolteur au primaire d'un transformateur dévolteur dont le rapport de spires primaire:secondaire est de 300:1. La résistance d'une petite ville, de 1,8 mΩ, est branchée à son secondaire.

       a) Quelle est la résistance de la ville vue à travers le transformateur dévolteur?

       b) Quelle est l'impédance du réseau aux bornes de l'alternateur?

       c) Quel est le courant débité par l'alternateur?

       d) Quelle est la puissance apparente fournie par l'alternateur?

       e) Quelle est la puissance réelle consommée par la ville?

       f) Quelle est la tension induite dans le stator de l'alternateur?

       g) Quel est le moment de force mécanique requis pour faire tourner le rotor de l'alternateur à vitesse constante?

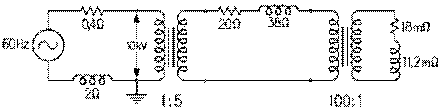                                                 (une phase)

9.15     Le stator d'un alternateur triphasé de 4 pôles crée une tension étoilée de 10 kV à 60 Hz aux bornes du primaire d'un transformateur survolteur dont le rapport de spires primaire:secondaire est de 1:5. La résistance interne de chaque phase du stator est de 0,4 Ω; sa réactance inductive, de 2 Ω. Une ligne de transmission, de 20 Ω de résistance et de 38 Ω de réactance inductive par phase, réunit le secondaire du chaque transformateur survolteur au primaire d'un transformateur dévolteur dont le rapport de spires primaire:secondaire est de 100:1. Une usine est branchée au secondaire des trois transformateurs dévolteurs. Son impédance aux bornes de chacun est de 18 mΩ de résistance et de 11,2 mΩ de réactance inductive.

       a) Quelle est l'impédance du réseau aux bornes de chaque phase de l'alternateur?

       b) Quelle est la tension étoilée induite dans le stator de l'alternateur?

       c) Quelle est la puissance apparente produite par l'alternateur?

       d) Quel est le moment de force développé par la turbine qui entraîne le rotor de l'alternateur?