Électroscope
CHAPITRE PRÉLIMINAIRE
QUELQUES CONCEPTS PRÉLIMINAIRES
Nous aurions vu dans le premier chapitre comment le concept de charge électrique est introduit, et comment Franklin prouve que celle-ci est conservée. Nous aurions également vu l'effet d'une charge sur une autre, son influence en un point et comment il est possible de charger un corps par influence ainsi que précisé la différence entre un conducteur et un isolant. Ces concepts vont tous nous être utiles dans ce chapitre, qui va nous introduire aux concepts de tension et de courant électriques.
Nous aurions vu plusieurs façons de déterminer si un corps est chargé ou non. Certes le meilleur appareil pour déterminer la charge est, jusqu'ici, la balance électrique de Coulomb. Mais celle-ci est peu commode: elle est en effet très délicate.
3.1 L'électroscope
Abraham Bennet (1750-1799) invente en 1787 un nouvel instrument pour, du moins à première vue, mesurer la charge d'un corps. Il le baptise électroscope, du grec pour voir la charge. Cet appareil existe sous plusieurs variantes, dont nous allons donner ici un des meilleurs modèles.
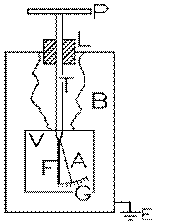
ÉlectroscopeNotre électroscope comprend un ensemble conducteur interne placé dans un boîtier rectangulaire B , presqu'entièrement métallique, muni d'une vitre V sur un de ses côtés pour voir son intérieur et d'un trou en son sommet. Le boîtier métallique est relié à la terre E . L'ensemble conducteur interne comprend une tige de bronze T à l'extrémité inférieure de laquelle se trouvent une feuille verticale de bronze fixe F et une feuille mobile très mince en or A ; il est relié à un plateau externe en bronze P. La tige T traverse le boîtier conducteur B en son sommet à travers un bouchon isolant L . Les feuilles de bronze fixe verticale F et d'or mobile A sont initialement verticales et parallèles à deux des côtés du boîtier métallique B mis à la terre. La vitre V se trouve sur un des deux autres côtés du boîtier, de telle sorte que celle-ci permette de voir tout mouvement de la feuille d'or A . L'angle que fait la feuille d'or par rapport à la verticale peut alors être lu sur des graduations G placées sur la vitre V.
(L'électroscope de Bennet avait deux feuilles d'or; le boîtier était en fait un bocal de verre dans lequel se trouvaient deux feuilles conductrices parallèles aux feuilles et mises à la terre, ce qui revient pratiquement au même.)
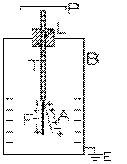
Si un électrophore chargé est placé sur le plateau P de l'électroscope, la feuille d'or va dévier de la verticale. Cela, parce que la charge de l'électrophore se répand, en quelque sorte, sur les deux feuilles F et A et que celles-ci, étant de même signe, vont se repousser. Mais il y a plus: ces feuilles vont attirer, de la terre sur les faces opposées du boîtier, des charges de signe opposé; et donc, non seulement la feuille d'or A est repoussée par la feuille fixe F , mais elle est attirée par les charges maintenant placées sur la surface interne du boîtier la plus proche d'elle. Ces charges de signe opposé sur la surface interne du boîtier attirent davantage des charges, de l'ensemble interne sur les feuilles F et A . L'instrument de Bennet permet donc de détecter des charges assez facilement.
3.2 La tension électrique
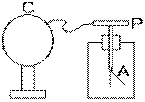
Volta se sert d'un instrument analogue en 1781. Mais voici qu'il l'utilise de façon quelque peu différente: à l'aide d'un fil conducteur, il relie le plateau P de l'électroscope à un point d'une sphère conductrice C chargée et isolée du sol. Il remarque une certaine déviation de l'angle que fait la feuille mobile A de l'appareil avec la verticale. Il remarque maintenant que la déviation de la feuille mobile A ne change pas lorsqu'il déplace son point de contact sur la sphère conductrice chargée C isolée du sol.
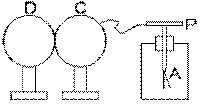
Il met maintenant une deuxième sphère métallique D, identique à la première mais initialement déchargée, en contact avec celle-ci. Il remarque que la feuille mobile A fait maintenant un angle avec la verticale qui est à peu près deux fois moindre qu'avant. Encore une fois, l'angle avec la verticale reste le même pour tout point de contact, et pour les deux sphères.
Volta cherche à comprendre ses résultats. Il part avec le principe de la conservation de la charge. Sa première sphère C avait une charge donnée. Celle-ci a dû en perdre une partie lorsqu'il l'a mise en contact avec le plateau de son électroscope, comme celui-ci doit en avoir reçu pour que sa feuille mobile dévie. Certes, la déviation angulaire de sa feuille A doit dépendre de sa charge. Quand il met les deux sphères en contact, la charge doit maintenant se répartir sur les deux sphères et l'électroscope: il y en a donc moins pour chacun, à peu près la moitié moins, et donc l'angle de déviation de la feuille d'or avec la verticale n'est plus que la moitié de ce qu'il était.
Mais les deux sphères en contact ne font-elles pas un seul corps électrisé conducteur? Et sa charge n'est-elle pas essentiellement la même que celle de la sphère conductrice originale?
L'électroscope, ainsi branché, ne mesure pas la charge du corps conducteur auquel son plateau est relié: en effet la charge est la même sur l'ensemble des deux sphères métalliques en contact que sur la sphère originale alors que la déviation angulaire est différente. Que mesure-t-il alors? Quelque chose qui a diminué de moitié lorsque deux corps conducteurs identiques ont porté la charge que l'un seulement portait. Ou, dit autrement, quelque chose qui diminue de moitié quand la charge du corps particulier C diminue de moitié.
La charge électrique placée sur la sphère C est d'un même signe: ses parties se repoussent donc; et ce, d'autant plus que la charge est grande. Les forces électriques qui cherchent à les repousser les unes des autres sont donc d'autant plus fortes que chacune des parties est fortement chargée. Mais les parties en question ne sont pas repoussées. Il faut donc qu'il existe une force de cohésion qui retienne chaque partie chargée sur la sphère.
La même chose se produit lorsqu'on suspend une charge à un ressort: des forces apparaissent dans ce dernier, qui cherchent à l'étirer; mais il y a une force de cohésion, sa tension, qui les contrecarre et maintient ensemble les parties du ressort. Cette tension requise doit être, pour un ressort donné, d'autant plus grande que la charge qu'il supporte est grande.
Volta décide donc d'appeler tension électrique Te cette "force" requise pour tenir ensemble la charge Q de la sphère, "force" qui est d'autant plus grande que la charge qui s'y trouve est grande
La tension électrique Te a donc diminué de moitié quand la charge Q de la sphère C a diminué de moitié.
Il remarque que la tension électrique a une différence importante d'avec la tension d'un ressort; alors que celle du ressort est toujours positive, la tension électrique est négative si la charge du corps est négative.
Volta reprend ses expériences. Lors de la charge d'une sphère conductrice C avec son électrophore, il remarque une étincelle entre l'électrophore et la sphère juste avant que ceux-ci ne se touchent. Après contact, le sphère conductrice reçoit une charge Q et donc a une tension électrique Te , mesurée comme une déviation angulaire de la feuille d'or de son électroscope. Il remarque qu'une seconde sphère D, déchargée, ne cause pas de déviation angulaire de la feuille d'or avec la verticale de son électroscope. Et, puisqu'elle est déchargée, elle n'a pas de tension électrique selon notre équation (3.2.1). Il amène la seconde sphère conductrice D en contact avec sa première: il remarque à nouveau une étincelle entre les deux sphères juste avant qu'elles se touchent. Il sait que l'étincelle indique le passage du fluide électrique d'un corps à l'autre. C'est donc l'indication d'un transfert de charge d'un corps à l'autre. Il remarque, encore une fois, que la déviation angulaire de la feuille d'or de son électroscope avec la verticale n'est plus que la moitié, situation dans laquelle la charge de l'ensemble des deux sphères est la même mais la tension électrique sur chaque est la moitié. Il remarque que la déviation angulaire de la feuille d'or de son électroscope avec la verticale ne change pas s'il éloigne les deux sphères l'une de l'autre et ce, quelle que soit la sphère reliée à son électroscope. Et, s'il les remet en contact, il n'y a pas d'étincelle entre elles juste avant le contact.
Volta peut donc conclure que son électroscope, mis en contact avec un corps conducteur, ne mesure pas sa charge mais bien sa tension électrique puisque c'est elle qui a diminué de moitié. Il peut conclure également qu'il n'y a pas de transfert de charge (vu qu'il n'y a pas d'étincelle) entre deux conducteurs qui ont même tension électrique. Ce qui est fort raisonnable, comme la force de tension électrique qui les retient est aussi forte sur l'une que sur l'autre; mais qu'il y a transfert de charge (vu la présence de l'étincelle) entre deux conducteurs qui n'ont pas même tension électrique, comme les forces de tension électrique ne sont pas égales. Ce n'est que lorsque les tensions électriques des deux corps en contact se seront égalisées que le mouvement de fluide électrique cessera.
Volta imagine alors une autre analogie de la tension électrique: la tension élastique de la membrane qui retient l'air à l'intérieur d'un ballon. Celle-ci équilibre la pression de l'air qui presse contre elle, tout comme la tension élastique du ressort équilibre le poids suspendu. Cette tension élastique doit être constante partout sur la membrane du ballon puisque la totalité de celle-ci subit la même pression de l'air. De même la tension électrique doit être partout constante sur la surface du conducteur puisqu'il y a même pression (de charges) électrique. Comme il existe souvent des points faibles sur les surfaces des membranes, points où se produisent à des pressions trop fortes des fuites d'air, il existe des points faibles sur les surfaces conductrices, points où se produisent à des pressions électriques trop fortes des fuites de fluide électrique.
Les aigrettes et les étoiles se produisent donc lorsque la pression électrique à la surface du corps conducteur excède la tension électrique possible en ce point de la surface: comme la tension électrique n'équilibre plus la pression électrique, le fluide fuit alors la surface.
Il s'ensuit de cela que toutes les parties d'un ensemble conducteur doivent sentir la même tension électrique. Toute la surface d'un corps ellipsoïde chargé doit être sous la même tension électrique; et c'est bien ce que l'électroscope indique: la déviation angulaire de sa feuille d'or d'avec la verticale reste la même quel que soit le point du corps électrisé conducteur en contact avec son plateau.
L'électroscope mesure donc la tension électrique du corps auquel il est relié. Mais celle-ci ne cause souvent qu'une très faible déviation de la feuille d'or, si faible qu'elle est très difficile à mesurer.
3.3 Le "condensateur" de Volta
Volta charge avec son électrophore une grosse bouteille de Leyde. Il remarque que la déviation de la feuille d'or de son électroscope est très faible lorsque la bouteille est reliée à son plateau, trop faible pour être bien mesurée. Son électroscope n'est pas assez sensible.
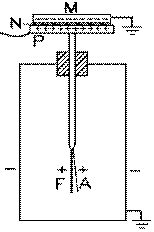
Aussi décide-t-il d'inventer en 1782 ce qu'il appelle le "condensateur". Une plaque métallique M , de dimensions un peu plus petites que celles du plateau métallique P de son électroscope, est recouverte, sur une surface, avec une mince couche de vernis N . Elle est ensuite reliée à la terre (et donc au boîtier de l'électroscope). Il la place sur le plateau de son électroscope, avec sa surface vernie N en contact avec ce dernier. Son "condensateur" comprend en fait trois éléments: le plateau conducteur P de l'électroscope, le vernis isolant N , et la plaque conductrice M placée sur le plateau.
Il se forme une étincelle juste avant qu'il ne relie sa bouteille de Leyde au plateau P de son électroscope, comme la tension électrique de la bouteille n'est pas la même que celle du plateau de l'électroscope. Puis, une fois que le fluide électrique a cessé de couler, la tension électrique est la même sur le plateau de l'électroscope et sur la bouteille de Leyde, et la feuille d'or de son électroscope dévie très légèrement puisque la charge Qe sur les feuilles F et A de l'électroscope est très faible. La tension Te de la bouteille de Leyde est devenue celle de l'électroscope; et ainsi, la charge Qe est apparue sur ses feuilles.
Les charges (disons positives) de la bouteille ne se sont pas seulement placées sur les feuilles F et A comme auparavant, mais également, et en plus grand nombre, sur la surface supérieure du plateau P devant la mince couche de vernis. En effet, les charges qui viennent se placer sur le plateau P attirent sur la plaque M des charges de signe opposé, qui viennent de la terre, comme celle-ci lui est reliée. Ces charges, ici négatives, attirent elles-mêmes de nouvelles charges positives de l'ensemble interne de l'électroscope relié au plateau. La très faible épaisseur du vernis N qui retient les charges de signe opposé sur leurs plaques P et M respectives fait que presque toutes les charges positives de l'ensemble viennent s'y condenser: d'où le terme condensateur inventé par Volta en 1782. L'effet d'attraction de charges de signe opposé est d'autant plus grand que la distance qui les sépare est plus faible; ce qui est le cas dans cette région, et non pas dans la zone interne du boîtier entre les feuilles F et A et les murs du boîtier qui leur sont parallèles.
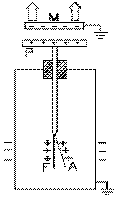
L'électroscope lui-même, le condensateur et la bouteille de Leyde sont tous reliés, et donc tous sous même tension, si faible que la feuille A ne bouge presque pas.
Volta débranche maintenant la bouteille de Leyde de l'ensemble condensateur-électroscope, dont la charge Q est principalement sur le condensateur (environ 99%) et légèrement sur les feuilles de l'électroscope (charge Qe d'environ 1% de la charge Q totale). Puis il soulève la plaque M du condensateur, plaque qui est reliée à la terre: la feuille A dévie davantage. Il l'enlève complètement: l'angle de déviation de sa feuille d'or A d'avec la verticale est agrandi par un facteur d'une centaine!
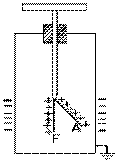
Volta sait que l'attraction des charges de signe opposé diminue avec la distance; en éloignant la plaque M de son condensateur de la plaque P , il se trouve à diminuer la condensation de charges sur la plaque P , puisque celles-ci peuvent aller sur les feuilles F et A . C'est ce qui se passe; et, à la limite, quand la plaque M a été éliminée, le condensateur a été éliminé et toute la charge Q est sur son électroscope. Puisque la charge sur les feuilles de l'électroscope est maintenant cent fois plus grande qu'avant, il s'ensuit que sa tension Te l'est également, et est donc plus facile à mesurer, puisque l'angle de déviation de la feuille A d'avec la verticale est plus facile à mesurer. Volta vient donc de mettre au point une méthode simple de mesurer de faibles tensions électriques.
______________________________
Nous aurions vu dans le chapitre trois qu'Oersted montre en 1819 qu'un courant électrique cause une force magnétique sur une boussole, et donc un champ magnétique. C'est ce champ magnétique qui va nous intéresser.
4.1 L'expérience de Biot et Savart
Biot et Savart mesurent en 1820 la grandeur de la force magnétique Fm subie par les pôles de leur boussole, suspendue à un fil, lorsque placée à une distance d d'un long fil rectiligne. Ils vérifient que le champ magnétique décrit bien des cercles, dont l'axe est le fil rectiligne parcouru par le courant électrique I , comme l'avait trouvé Oersted. Ils observent que le champ magnétique B trouvé dans la région centrale du fil rectiligne
va comme l'inverse de la distance d au fil pour un courant I donné, et qu'il est proportionnel au courant, à une distance donnée.
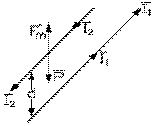Courants parallèlesAmpère montre aussitôt que deux longs fils rectilignes, proches et parallèles, s'attirent si leurs courants sont de même sens, et se repoussent s'ils sont de sens opposés. Pour ce faire, il fixe un fil rectiligne mobile, de longueur L2 , au-dessus d'un autre fixe et plus long, de telle sorte qu'il ne surplombe que la région centrale du fil fixe. Il ajuste le fil mobile de longueur L2 à une distance d du premier à l'aide d'un balancier.
Il fait passer maintenant un courant I1 dans le fil fixe et un courant I2 dans le fil mobile. Il remarque que les deux fils s'éloignent si les courants sont de sens contraires; c'est donc que le fil mobile subit une force magnétique de répulsion Fm . Il place une petite masse m sur le fil mobile de telle sorte que celui-ci revienne à sa position originale, à la distance d du fil fixe. La force magnétique Fm est alors contrée exactement par le poids P de la petite masse m . Il peut donc la mesurer. Refaisant cette expérience pour des courants différents qu'il peut additionner, et pour des distances d différentes ainsi que pour des longueurs L2 différentes, il trouve que
la force magnétique subie par le fil mobile de longueur L2 est proportionnelle à celle-ci; qu'elle est inversement proportionnelle à sa distance d du fil fixe; et proportionnelle au produit des courants I1 et I2 . La constante km vaut, par définition de l'unité de courant, 2⋅10 - 7 N / A 2.
Biot et Savart ont montré que le fil rectiligne long, parcouru par le courant I1 , cause un champ magnétique B1 , constant là où se trouve le fil mobile de longueur L2 parcouru par un courant I2 , et est , par notre équation (4.1.1), proportionnel au courant I1 et inversement proportionnel à la distance d . Il s'ensuit que la force magnétique subie par le fil mobile est proportionnelle au champ magnétique B1 , causé par le courant I1 à une distance d , soit là où se trouve le fil mobile. Si nous assimilons la constante km au champ magnétique B1 , l'équation trouvée par Ampère devient
avec
pour l'équation du champ magnétique dû à un long fil. L'unité de champ magnétique le est le tesla, noté T , et est donnée par le produit de ( N / A 2 ) ⋅ ( A / m ) = N / A m . Nous verrons plus tard d'où provient ce nom.
Du travail de Biot et Savart (et un peu de celui d'Ampère), nous trouvons que le champ magnétique B , à une distance d d'un long fil rectiligne parcouru par un courant I , est
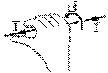
et décrit, comme nous avons déjà vu, des cercles autour de son axe, cercles donnés par la règle suivante: si le pouce de notre main droite pointe dans le même sens que le vecteur courant qui circule dans ce long fil rectiligne, le sens de rotation de son vecteur champ magnétique est donné par le sens de rotation dans lequel pointent les doigts de cette main.
4.2 La force magnétique d'Ampère
a) équation vectorielle de la force magnétique
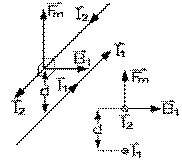Deux vues des vecteurs
courant, champ et forceSur notre croquis, le champ magnétique B1 ( dû au courant I1 qui s'éloigne de nous dans le fil fixe, là où se trouve le fil rectiligne de longueur L2 , parcouru par le courant I2 qui vient vers nous) est vers la droite, selon notre règle, puisque le point est juste au-dessus du fil fixe. La force magnétique subie par le fil mobile est, avons-nous vu, une force de répulsion: elle est donc vers le haut.
La force magnétique est un vecteur, perpendiculaire à la fois au vecteur champ magnétique et au vecteur courant , dont les grandeurs apparaissent dans notre équation (4.1.5). Ces derniers vecteurs sont, également, perpendiculaires entre eux.
Le symbole d'un vecteur qui sort de la feuille est un point (la tête acérée d'une flèche) encerclé; celui d'un vecteur qui s'enfonce dans la feuille, une croix de Saint-André (un "x") (la queue d'une flèche) encerclée.
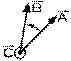
Le produit de deux vecteurs qui est lui-même un vecteur, perpendiculaire au plan dans lequel se trouvent ceux-ci, est dit produit vectoriel; sa grandeur est, par définition, donnée par la grandeur de ces vecteurs fois le sinus de l'angle qu'ils font entre eux. Dans notre cas, la valeur du sinus est l'unité puisque cet angle est droit. Le sens du vecteur résultant d'un produit vectoriel est donné par la règle de la main droite: celle-ci est placée de telle sorte que, avec la paume de la main droite ouverte, les quatre doigts soient superposés sur le premier vecteur du produit; la main est ensuite fermée de telle sorte que les quatre doigts se dirigent vers le second vecteur du produit vectoriel. Le pouce indique alors le sens du vecteur produit, perpendiculaire au plan dans lequel se trouvent les deux autres.
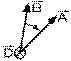
Le produit vectoriel n'est pas commutatif; c'est-à-dire que le produit vectoriel d'un vecteur par le vecteur n'est pas égal au produit vectoriel du vecteur par le vecteur : les vecteurs et ont des sens opposés quoique des grandeurs égales.
Le vecteur force magnétique satisfait les conditions d'un produit vectoriel des vecteurs et puisque sa direction est bien perpendiculaire aux deux et sa grandeur est bien donnée par le produit de leurs grandeurs dans ce cas-ci où l'angle entre les deux est droit. Son sens est celui trouvé expérimentalement si le vecteur force magnétique
est donné par la rotation du vecteur courant vers le vecteur champ magnétique .
Ampère remarque, encore en 1820, que si l'aimant de fer est attiré par sa bobine qui porte un courant, celle-ci l'est également par lui: la loi d'action-réaction de sir Isaac Newton s'applique encore ici.
b) les expériences de Faraday
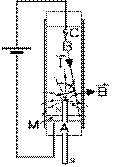
Faraday produit en 1821 deux expériences sur la force magnétique d'Ampère. Dans sa première, une broche B de métal, un conducteur, est suspendue à un crochet C conducteur au-dessus d'un bain de mercure M de telle sorte que le bas de la broche le touche. Le mercure est un liquide conducteur. Le crochet conducteur C est relié au pôle positif d'une pile; le bain de mercure M , au pôle négatif. Un courant I circule alors dans la broche B vers le bas. Le pôle nord d'un aimant vertical fixe A est placé au milieu du bain de mercure M de telle sorte qu'il dépasse juste d'un peu. Des segments de la broche conductrice B parcourue par le courant I subissent alors son champ magnétique B de telle sorte que la force magnétique soit, dans le cas de notre croquis, vers nous: la broche B tourne donc autour du pôle de l'aimant A . Ceci constitue le prototype du moteur électrique.
Dans une seconde expérience, produite tout de suite après, la broche métallique
B est fixée au centre du bain de mercure M . Son courant est encore vers le bas. Le pôle
sud de l'aimant A est attaché par une courte corde à un point C au centre du fond du
bain de
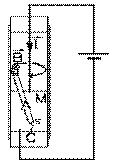
mercure M . L'aimant A cherche à flotter dans le mercure, plus lourd que lui: son pôle nord est donc à l'air libre. Le courant cause un champ magnétique qui s'enfonce dans la feuille là où se trouve le pôle nord de l'aimant A , causant donc une force magnétique qui s'enfonce dans la feuille: l'aimant A tourne alors autour de la broche B .
Davy, en 1821, montre qu'un arc électrique dévie sous l'effet du champ magnétique comme le prévoit la force magnétique d'Ampère. Ce qui montre, également, que l'arc électrique est bien la manifestation d'un courant électrique.
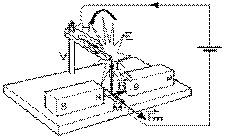
c) la roue de Barlow
En 1822, Peter Barlow (1776-1862) produit ce qui pourrait être appelé le premier moteur électrique. Il suspend, à un support conducteur horizontal H lui-même placé sur une tige isolante verticale V , une roue métallique E , en forme d'étoile, de telle sorte qu'elle puisse tourner sur un axe horizontal. Le bas de la roue E est placé entre des pôles nord et sud d'aimants. L'extrémité des étoiles de la roue E peut baigner dans un bain de mercure M . Il remarque que sa roue E tourne s'il connecte le support horizontal H au pôle positif d'une pile électrique, et l'autre pôle, au bain de mercure M . Le courant descend alors dans la roue si le bas d'une branche d'étoile E baigne dans le mercure M . Le vecteur courant électrique est alors perpendiculaire au vecteur champ magnétique entre les deux pôles des aimants, ce qui cause la force magnétique d'Ampère, et donc la rotation de la roue E . Puisque le courant ne circule dans la roue E que si le bout d'une branche baigne dans le mercure M , la force magnétique n'existe que de façon intermittente avec ce montage.
Il remarque, peu de temps après, qu'un disque métallique, dont la base baigne dans le mercure, tourne mieux encore puisque le courant n'est plus intermittent.
____________________
_________________________________
_______________________________
4.11 Effet d'un courant sur le fer
Nous aurions déjà remarqué dans le chapitre premier que le fer doux s'aimante une fois placé aux alentours d'un aimant permanent; et qu'il a tendance à s'orienter dans le sens du champ magnétique qui existe là où il se trouve, s'il a la forme d'une aiguille. Aussi de fines parcelles de limaille de fer doux s'orientent alors toutes selon le sens du vecteur champ magnétique, présent là où elles se trouvent. Qui plus est, comme elles s'attirent l'une l'autre, elles ont tendance à se placer à la suite, à la queue-leu-leu, suivant la direction du champ magnétique local. Elles se trouvent ainsi à rendre visible ce que Faraday baptise en 1831 les lignes de force magnétique: la forme du champ magnétique dû, dans notre cas, à un aimant permanent.
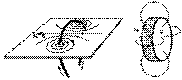
En 1820, Arago, comme Ampère, montre qu'une bobine de courant cause l'aimantation d'une aiguille de fer doux. Mais en plus, que celle-ci agit sur la limaille de fer doux tout comme l'aimant permanent, et y cause des formes très similaires.
Évidemment, la différence est qu'il est possible de voir la disposition de la limaille de fer à l'intérieur d'une bobine mince alors qu'il est impossible de voir le champ magnétique à l'intérieur d'un aimant. Pour Ampère, le fait que les lignes de force magnétique aient la même forme à l'extérieur est la preuve qu'un aimant permanent est en fait une bobine de courant; qu'il y a en fait des courants qui circulent constamment à l'intérieur de l'aimant permanent. Et qu'il doit y avoir, en son intérieur, des lignes de force magnétique, tout comme il y en a dans le cas de la bobine de courant. Les pôles magnétiques n'agissent pas vraiment comme des charges magnétiques, d'où émanerait le champ magnétique, comme nous avions vu dans notre chapitre premier. Les lignes de champ magnétique ne divergeant pas de "charges magnétiques", le flux magnétique net est nul.
En 1822, Ampère, avons-nous vu, crée le solénoïde. Il place en son intérieur une aiguille d'acier, du fer aigre. Puis il branche son solénoïde à une pile électrique, produisant ainsi en son intérieur un champ magnétique, comme nous venons de voir. Il coupe ensuite le courant, et sort son aiguille d'acier de l'intérieur du solénoïde: celle-ci est maintenant magnétisée, et mieux que par la méthode du double-toucher. L'aiguille, faite de fer aigre, demeure magnétisée, comme nous avons déjà vu dans notre premier chapitre.
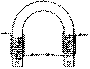
Sturgeon s'intéresse, à partir de 1821, à l'expérience d'Arago de 1820. En 1825, il forge un fer doux en forme de fer à cheval et le recouvre d'une couche de vernis. Il roule ensuite, en spirales éloignées les unes des autres, 16 tours de fil de cuivre dénudé. Il lance un courant dans son fil, magnétisant ainsi son fer doux: il vient de créer le premier électro-aimant pratique. Il place alors ce dernier juste au-dessus d'une masse de fer de 5 kg: celle-ci, aussitôt attirée par l'électro-aimant, est soulevée du sol. Elle retombe aussitôt que le courant est coupé, puisque le fer doux ne conserve pas alors son aimantation.
Joseph Henry (1797-1878) produit en 1828 des électro-aimants plus puissants. Il suppose que le champ magnétique du fer doux grandit avec le champ magnétique produit par le courant. Aussi augmente-t-il grandement le nombre de tours de fil roulés sur le fer doux. Au lieu d'utiliser du fil conducteur dénudé comme Sturgeon, il utilise du fil recouvert de soie, qu'il peut donc rouler en spires serrées. Le progrès dans la construction des électro-aimants se poursuit alors rapidement, sujet sur lequel nous reviendrons plus tard. Mais terminons ce chapitre avec l'étude du galvanomètre à cadre mobile.
4.12 Galvanomètres à cadre mobile
a) galvanomètre de Sturgeon
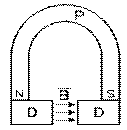
Sturgeon bâtit en 1836 le premier galvanomètre à cadre mobile. Il fabrique d'abord un aimant permanent P en forme de fer à cheval. Il place, à chaque pôle de son aimant, un noyau de fer doux D dit pièce polaire afin de réduire la distance dans l'air. Ces deux morceaux de fer doux D deviennent magnétisés par induction. Il remarque, en plaçant de la limaille de fer dans la région avoisinante, que les lignes de force magnétique sont essentiellement parallèles entre elles, d'un pôle à l'autre, dans la zone entre ceux-ci,
Il roule alors, sur un cadre de bois, un long fil conducteur mince, recouvert de soie. Il suspend, à l'aide d'une extrémité du fil conducteur, le cadre entre les deux pièces polaires P de telle sorte que celui-ci soit parallèle aux lignes de force magnétique. L'autre extrémité du fil conducteur est reliée à une borne.
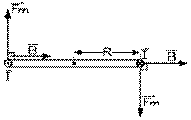
Il fait passer un courant I dans le fil conducteur en partie roulé sur le cadre. La force magnétique d'Ampère Fm se fait sentir sur chaque segment vertical de fil de longueur L , trouvé dans la zone entre les noyaux où il existe un champ magnétique B perpendiculaire au courant I . Il y en a N contigus au pôle nord, et N contigus au pôle sud, puisqu'il y a N enroulements de fil conducteur. Ces forces magnétiques, à angle droit avec le cadre, appliquées à une distance R de l'axe de rotation, causent toutes des moments de force égaux. Le moment de force magnétique résultant MR dû aux deux moments de force magnétique Mm
doit alors être compensé par un moment de torsion Mt en tordant la partie du fil conducteur qui supporte le cadre d'un angle θ pour le ramener à sa position originale, le long des lignes de champ magnétique.
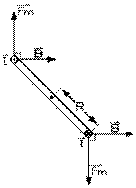
Évidemment, un des problèmes avec pareil montage est de repérer la position originale. Il faut, pour ce faire, placer un marqueur sur le cadre. Johann Christian Poggendorff (1796-1877) avait déjà, en 1826, placé un petit miroir sur la partie mobile de son galvanomètre afin de le rendre plus sensible. Une très faible rotation de ce dernier cause une déviation importante de la lumière qu'il réfléchit sur un mur éloigné.
Nous avons vu, dans notre section 4.5, le galvanomètre boussole de tangentes de Pouillet. Ce galvanomètre a, entre autres avantages, celui de ne pas exiger de l'opérateur de ramener la partie mobile à sa position originale en tordant quelque fil. Nous allons en voir deux autres ayant ce même avantage.
Le galvanomètre de Sturgeon tourne de lui-même quand il est parcouru par un courant. Et développe de lui-même un moment de torsion lors de sa rotation. Mais, comme la force magnétique n'est plus alors à angle droit avec le cadre, les moments de force magnétique varient avec l'angle, ce qui est embêtant.
b) galvanomètre d’Arsonval
Ce problème peut être éliminé complètement en donnant aux surfaces des pièces polaires D , qui sont contiguës au cadre mobile C , une surface cylindrique d'une part, et en plaçant sur l'axe de rotation du cadre un noyau supplémentaire de fer doux E , d'autre part. La région, dans l'air, dans laquelle tourne le cadre est alors fort petite. Cette région est dite entrefer. Le noyau cylindrique E est alors aimanté par induction et le champ magnétique dans l'entrefer est alors trouvé radial et constant. Le vecteur champ magnétique dans l'entrefer est alors toujours tel que la force magnétique est perpendiculaire au plan du cadre. L'équation (4.12.1) s'applique maintenant pour tout angle tant et aussi longtemps que le cadre demeure dans l'entrefer. Evidemment, le cadre mobile C ne peut plus être plein. Aussi le fil conducteur recouvert d'un isolant est roulé sur un cadre creux de cuivre.
Ces modifications au galvanomètre à cadre mobile de Sturgeon, qui datent de 1882, sont dues à Marcel Deprez (1843-1918) et Arsène d'Arsonval (1851-1940). Le courant qui circule dans le cadre mobile est alors directement proportionnel à l'angle de rotation du cadre, qui n'est rien d'autre que l'angle de rotation de son fil de torsion conducteur.
c) galvanomètre Weston
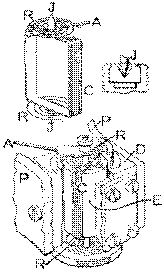
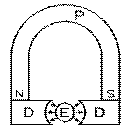
En 1888, la firme américaine Weston modifie le montage de d'Arsonval pour produire le premier galvanomètre portatif de qualité. Les modifications sont essentiellement en nombre de trois: le cadre mobile C tourne maintenant sur des vis à pierre J ; le fil de torsion conducteur est remplacé par des ressorts conducteurs en spirale R et l'indicateur est formé d'une longue aiguille A placée à angle droit avec le cadre. Cette aiguille va indiquer une position sur un cadran placée à une certaine distance de là. L'aimant utilisé a la forme d'un fer à cheval dont les extrémités, ses pôles P , sont parallèles et reserrées. Les vis à pierre sont solides mais ne s'opposent pas au mouvement de rotation du cadre. Le courant passe dans les spires roulées sur le cadre par l'intermédiaire des ressorts en spirale conducteurs.
Le cadre en rotation autour du noyau de fer doux comprend donc N spires. Sa longueur Lc , soit son côté parallèle à son axe de rotation, doit être plus grande que la longueur L du noyau lui-même. La grandeur de la force magnétique Fm subie par un de ses côtés de longueur Lc est
puisque le champ magnétique B n'existe que dans l'entrefer, dont la longueur L est la longueur du noyau et la largeur des pièces polaires, ainsi que le montre clairement le croquis ci-contre. Cette force magnétique Fm est alors à angle droit avec le plan du cadre mobile.
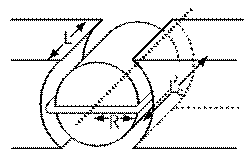
Puisqu'il n'y a pas de champ magnétique dans l'air ailleurs que dans l'entrefer, il n'y a aucune force magnétique exercée sur les côtés du cadre qui sont perpendiculaires à son axe de rotation.
La largeur du cadre mobile est deux fois la distance R qu'il y a entre le segment trouvé dans l'entrefer et son axe. Le moment de force Mm magnétique exercé sur un des côtés du cadre trouvé dans l'entrefer est donné
par le produit de la force magnétique subie Fm sur une longueur L de sa longueur Lc par son bras de levier R .